题目内容
17. 如图,已知四边形ABCD是平行四边形,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE,试判断四边形AECF是什么样的四边形?写出你的结论并予以证明.
如图,已知四边形ABCD是平行四边形,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE,试判断四边形AECF是什么样的四边形?写出你的结论并予以证明.
分析 根据垂直的定义得出∠AEF=∠CFE=90°,利用内错角相等两直线平行可得AE∥CF,再根据平行四边形的性质证明△ABE≌△CDF,根据全等三角形对应边相等可得AE=CF,然后根据有一组对边平行且相等的四边形是平行四边形即可证明.
解答 解:四边形AECF是平行四边形.理由如下:
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AEF=∠CFE=90°,
∴AE∥CF(内错角相等,两直线平行),
在平行四边形ABCD中,AB=CD,AB∥CD,
∴∠ABE=∠CDF,
在△ABE与△CDF中,
$\left\{\begin{array}{l}{∠ABE=∠CDF}\\{∠AEB=∠CFD=90°}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△CDF(AAS),
∴AE=CF,
∴四边形AECF是平行四边形(有一组对边平行且相等的四边形是平行四边形).
点评 本题考查了平行四边形的性质与判定,全等三角形的判定与性质,利用三角形全等证明得到AE=CF是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
7.下列图案中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.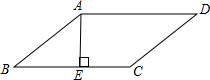 如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则?ABCD的周长为( )
如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则?ABCD的周长为( )
 如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则?ABCD的周长为( )
如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则?ABCD的周长为( )| A. | 4+2$\sqrt{2}$ | B. | 12+6$\sqrt{2}$ | C. | 2+2$\sqrt{2}$ | D. | 2+$\sqrt{2}$或12+6$\sqrt{2}$ |
7.下列计算不正确的是( )
| A. | 3$\sqrt{3}$$+5\sqrt{3}=8\sqrt{3}$ | B. | $\sqrt{14a}•\sqrt{7}=7\sqrt{2a}$ | C. | $\sqrt{8}-\sqrt{6}=\sqrt{2}$ | D. | $\sqrt{60a}÷\sqrt{5}=2\sqrt{3a}$ |
 如图,?ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,?ABCD满足矩形条件时,能判断四边形CODE是菱形.
如图,?ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,?ABCD满足矩形条件时,能判断四边形CODE是菱形.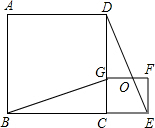 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列4个结论:
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列4个结论: 如图,已知在平行四边形ABCD中,对角线AC与BD交于点O,且BD⊥CD,若AD=13,CD=5,则BO的长度为6.
如图,已知在平行四边形ABCD中,对角线AC与BD交于点O,且BD⊥CD,若AD=13,CD=5,则BO的长度为6.


