题目内容
20.若正多边形的一个内角等于120°,则这个正多边形的边数是6.分析 多边形的内角和可以表示成(n-2)•180°,因为所给多边形的每个内角均相等,故又可表示成120°n,列方程可求解.此题还可以由已知条件,求出这个多边形的外角,再利用多边形的外角和定理求解.
解答 解:解法一:设所求正n边形边数为n,
则120°n=(n-2)•180°,
解得n=6;
解法二:设所求正n边形边数为n,
∵正n边形的每个内角都等于120°,
∴正n边形的每个外角都等于180°-120°=60°.
又因为多边形的外角和为360°,
即60°•n=360°,
∴n=6.
故答案为:6.
点评 本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
11.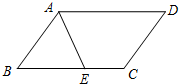 如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E.则线段BE、EC的长度分别为( )
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E.则线段BE、EC的长度分别为( )
 如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E.则线段BE、EC的长度分别为( )
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E.则线段BE、EC的长度分别为( )| A. | 2和3 | B. | 3和2 | C. | 4和1 | D. | 1和4 |
12.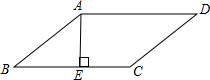 如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则?ABCD的周长为( )
如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则?ABCD的周长为( )
 如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则?ABCD的周长为( )
如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则?ABCD的周长为( )| A. | 4+2$\sqrt{2}$ | B. | 12+6$\sqrt{2}$ | C. | 2+2$\sqrt{2}$ | D. | 2+$\sqrt{2}$或12+6$\sqrt{2}$ |
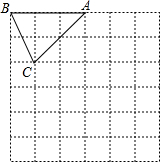 如图所示,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上.将△ABC向下平移2个单位得到△A1B1C1,然后将△A1B1C1绕点C1顺时针旋转90°得到△A2B2C1.
如图所示,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上.将△ABC向下平移2个单位得到△A1B1C1,然后将△A1B1C1绕点C1顺时针旋转90°得到△A2B2C1. 如图,?ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,?ABCD满足矩形条件时,能判断四边形CODE是菱形.
如图,?ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,?ABCD满足矩形条件时,能判断四边形CODE是菱形.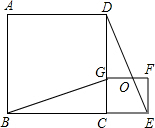 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列4个结论:
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列4个结论: 如图,已知在平行四边形ABCD中,对角线AC与BD交于点O,且BD⊥CD,若AD=13,CD=5,则BO的长度为6.
如图,已知在平行四边形ABCD中,对角线AC与BD交于点O,且BD⊥CD,若AD=13,CD=5,则BO的长度为6. 如图所示的平面纸能围成正方体盒子,请把与面A垂直的面用图中字母表示出来是B、C、E、F.
如图所示的平面纸能围成正方体盒子,请把与面A垂直的面用图中字母表示出来是B、C、E、F.