题目内容
9．某旅游景点的游客人数逐年增加，据有关部门统计，2014年约为21万人次，若2016年约为27万人次，设游客人数年平均增长率为x，则下列方程中正确的是（ ）| A． | 20（1+2x）=27 | B． | 27（1+x）2=21 | ||
| C． | 21（1+x）2=27 | D． | 21+21（1+x）+20（1+x）2=27 |
分析 增长率问题，一般用增长后的量=增长前的量×（1+增长率），参照本题，如果游客人数的年平均增长率为x，根据2014年约为21万人次，预计2016年约为27万人次，即可得出方程．
解答 解：设游客人数的年平均增长率为x，
则2015的游客人数为：21×（1+x）
2016的游客人数为：21×（1+x）2．
那么可得方程：21（1+x）2=27．
故选：C．
点评 本题考查了由实际问题抽象出一元二次方程，解此类题一般是根据题意分别列出不同时间按增长率所得游客人数与预计游客人数相等的方程．
练习册系列答案
相关题目
19．
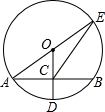如图所示，在⊙O中，半径OD⊥弦AB于点C，连接AO并延长交⊙O于点E，连接EC，若AB=8，CD=2，则EC的长度为（ ）
如图所示，在⊙O中，半径OD⊥弦AB于点C，连接AO并延长交⊙O于点E，连接EC，若AB=8，CD=2，则EC的长度为（ ）| A． | 2$\sqrt{5}$ | B． | 8 | C． | 2$\sqrt{10}$ | D． | 2$\sqrt{13}$ |
如图，BD是△ABC边AC的中线，点E在BC上，BE=$\frac{1}{2}$EC，△AED的面积是3，则△BED的面积是1.5．
4．已知五边形ANCDE∽五边形A1B1C1D1E1，五边形ABCDE的最短边为2，最长边为6，五边形A1B1C1D1E1，的最长边是12，则五边形A1B1C1D1E1的最短边是（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 8 |
14．某商品的原价是每件x元，在销售时每件加价20元，再降价15%，则现在每件的售价是（ ）元．
| A． | 15%x+20 | B． | （1-15%）x+20 | C． | 15%（x+20） | D． | （1-15%）（x+20） |
18．如果ab=cd，则下列比例式中不一定成立的是（ ）
| A． | $\frac{a}{c}$=$\frac{d}{b}$ | B． | $\frac{a}{d}$=$\frac{c}{b}$ | C． | $\frac{a}{c}$=$\frac{b}{d}$ | D． | $\frac{c}{a}$=$\frac{b}{d}$ |
19．
如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（ ）
如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（ ）| A． | BD=CD | B． | AB=AC | C． | ∠B=∠C | D． | ∠BDA=∠CDA |