题目内容
19.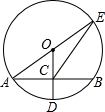 如图所示,在⊙O中,半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC,若AB=8,CD=2,则EC的长度为( )
如图所示,在⊙O中,半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC,若AB=8,CD=2,则EC的长度为( )| A. | 2$\sqrt{5}$ | B. | 8 | C. | 2$\sqrt{10}$ | D. | 2$\sqrt{13}$ |
分析 首先连接BE,由⊙O的半径OD⊥弦AB于点C,AB=8,CD=1,根据垂径定理可求得AC=BC=4,然后设OA=x,利用勾股定理可得方程:42+(x-1)2=x2,则可求得半径的长,继而利用三角形中位线的性质,求得BE的长,又由AE是直径,可得∠B=90°,继而求得答案.
解答 解:连接BE,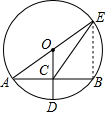
∵⊙O的半径OD⊥弦AB于点C,AB=8,
∴AC=BC=4,
设OA=x,
∵CD=2,
∴OC=x-2,
在Rt△AOC中,AC2+OC2=OA2,
∴42+(x-2)2=x2,
解得:x=5,
∴OA=OE=5,OC=3,
∴BE=2OC=6,
∵AE是直径,
∴∠B=90°,
∴CE=$\sqrt{B{C}^{2}+B{E}^{2}}$=2$\sqrt{13}$,
故选:D.
点评 此题考查了圆周角定理、垂径定理、勾股定理以及三角形中位线的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
9. 如图,直线a∥b,直线c与直线a、b分别相交于点A、B,AD⊥b,垂足为D,若∠1=37°,则∠2=( )
如图,直线a∥b,直线c与直线a、b分别相交于点A、B,AD⊥b,垂足为D,若∠1=37°,则∠2=( )
 如图,直线a∥b,直线c与直线a、b分别相交于点A、B,AD⊥b,垂足为D,若∠1=37°,则∠2=( )
如图,直线a∥b,直线c与直线a、b分别相交于点A、B,AD⊥b,垂足为D,若∠1=37°,则∠2=( )| A. | 53° | B. | 63° | C. | 37° | D. | 67° |
10.甲、乙、丙、丁四名选手参加200米决赛,赛场共设1,2,3,4四条跑道,选手以随机抽签的方式决定各自的跑道,若甲首先抽签,则甲抽到第1道的概率是( )
| A. | 0 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
7.-$\frac{1}{3}$的倒数是( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
4.点P1(1,y1),点P2(3,y2)是直线y=-4x+3上的两个点,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1≥y2 | C. | y1>y2 | D. | y1=y2 |
11.若a2+2a=1,则3a2+6a-2的值是( )
| A. | -1 | B. | 1 | C. | 4 | D. | 2 |
9.某旅游景点的游客人数逐年增加,据有关部门统计,2014年约为21万人次,若2016年约为27万人次,设游客人数年平均增长率为x,则下列方程中正确的是( )
| A. | 20(1+2x)=27 | B. | 27(1+x)2=21 | ||
| C. | 21(1+x)2=27 | D. | 21+21(1+x)+20(1+x)2=27 |




 在正方体的表面上画有图(1)中所示的线,图(2)是其展开图的示意图,但只在A面上画有线,那么将图1中剩余两个面中的线画入图(2)中,画法正确的是( )
在正方体的表面上画有图(1)中所示的线,图(2)是其展开图的示意图,但只在A面上画有线,那么将图1中剩余两个面中的线画入图(2)中,画法正确的是( )


