题目内容
17.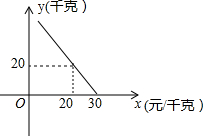 某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
分析 (1)由图象过点(20,20)和(30,0),利用待定系数法求直线解析式;
(2)每天利润=每千克的利润×销售量.据此列出表达式,运用函数性质解答.
解答 解:(1)设y=kx+b,由图象可知,
$\left\{\begin{array}{l}{20k+b=20}\\{30k+b=0}\end{array}\right.$,
解之,得:$\left\{\begin{array}{l}{k=-2}\\{b=60}\end{array}\right.$,
∴y=-2x+60;
(2)p=(x-10)y
=(x-10)(-2x+60)
=-2x2+80x-600,
∵a=-2<0,
∴p有最大值,
当x=-$\frac{80}{-2×2}$=20时,p最大值=200.
即当销售单价为20元/千克时,每天可获得最大利润200元.
点评 此题主要考查了待定系数法求一次函数解析式以及求二次函数最值等知识,解题的关键是理解题意,根据题意求得函数解析式,注意待定系数法的应用,注意数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12. 学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
 学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )| A. | 2 | B. | 2.8 | C. | 3 | D. | 3.3 |
2.同时抛掷两枚质地均匀的硬币,则下列事件发生的概率最大的是( )
| A. | 两正面都朝上 | B. | 两背面都朝上 | ||
| C. | 一个正面朝上,另一个背面朝上 | D. | 三种情况发生的概率一样大 |
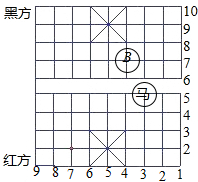 观察中国象棋的棋盘,其中红方“马”的位置可以用一个数对(3,5)来表示,红“马”走完“马3进四”后到达B点,则表示B点位置的数对是:(4,7).
观察中国象棋的棋盘,其中红方“马”的位置可以用一个数对(3,5)来表示,红“马”走完“马3进四”后到达B点,则表示B点位置的数对是:(4,7).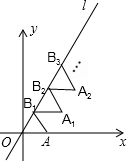 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标是($\frac{2017}{2}$,$\frac{2015\sqrt{3}}{2}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标是($\frac{2017}{2}$,$\frac{2015\sqrt{3}}{2}$).

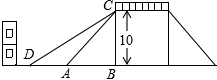 如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)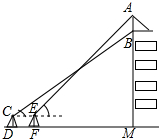 为了弘扬九十五中学办学理念,我校将“立己立人,尽善尽美”的校训印在旗帜上,放置在教学楼的顶部(如图所示).小华在教学楼前空地上的点D处,用1米高的测角仪CD,从点C测得旗帜的底部B的仰角为37°,然后向教学楼正方向走了4.8米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.若教学楼高BM=19米,且点A、B、M在同一直线上,求旗帜AB的高度(参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75.
为了弘扬九十五中学办学理念,我校将“立己立人,尽善尽美”的校训印在旗帜上,放置在教学楼的顶部(如图所示).小华在教学楼前空地上的点D处,用1米高的测角仪CD,从点C测得旗帜的底部B的仰角为37°,然后向教学楼正方向走了4.8米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.若教学楼高BM=19米,且点A、B、M在同一直线上,求旗帜AB的高度(参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75.