题目内容
7. 如图,平面直角坐标系中,点A的坐标(-3,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD
如图,平面直角坐标系中,点A的坐标(-3,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是3个单位长度;△AOC与△BOD关于直线对称,则对称轴是y;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是120度
(2)连结AD,交y轴于点E,求点E的坐标.
分析 (1)由点A的坐标为(-3,0),根据平移的性质得到△AOC沿x轴向右平移3个单位得到△OBD,则△AOC与△BOD关于y轴对称;根据等边三角形的性质得∠AOC=∠BOD=60°,则∠AOD=120°,根据旋转的定义得△AOC绕原点O顺时针旋转120°得到△DOB;
(2)连接AD,证明∠ADB=90°,再由△AOE∽△ADB,求出OE的长即可.
解答 解:(1)∵点A的坐标为(-3,0),
∴△AOC沿x轴向右平移3个单位得到△OBD;
∴△AOC与△BOD关于y轴对称;
∵△AOC为等边三角形,
∴∠AOC=∠BOD=60°,
∴∠AOD=120°,
∴△AOC绕原点O顺时针旋转120°得到△DOB.
故答案为:3;y轴;120;
(2)如图,∵OA=OD,∠BOD=60°,
∴∠ADO=30°,
∴∠ADB=90°
∵AB=6,BD=3,
∴AD=3$\sqrt{3}$,
∵△AOE∽△ADB,
∴$\frac{AO}{AD}=\frac{OE}{BD}$
∴OE=$\sqrt{3}$,
∴点E的坐标为:(0,$\sqrt{3}$).
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的性质、轴对称的性质、平移的性质以及相似三角形的判定与性质.第2小题发现△AOE∽△ADB是解决问题的关键.

练习册系列答案
相关题目
19. 如图,△ABC绕点A逆时针旋转40°后得到△ADF,且点D在BC边上,则∠B的度数为( )
如图,△ABC绕点A逆时针旋转40°后得到△ADF,且点D在BC边上,则∠B的度数为( )
 如图,△ABC绕点A逆时针旋转40°后得到△ADF,且点D在BC边上,则∠B的度数为( )
如图,△ABC绕点A逆时针旋转40°后得到△ADF,且点D在BC边上,则∠B的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
17.函数y=$\frac{\sqrt{x-1}}{{x}^{2}-4}$中自变量x的取值范围是( )
| A. | x≥1 | B. | x≥1且x≠±2 | C. | x≠±2 | D. | x≥1且x≠2 |
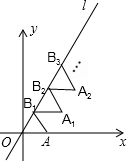 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标是($\frac{2017}{2}$,$\frac{2015\sqrt{3}}{2}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标是($\frac{2017}{2}$,$\frac{2015\sqrt{3}}{2}$).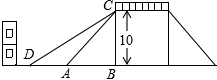 如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)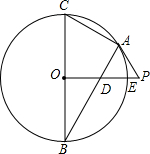 如图,已知PA与圆O相切于点A,直径BC⊥OP,线段OP与圆O交于点E,连接AB交PO于点D.
如图,已知PA与圆O相切于点A,直径BC⊥OP,线段OP与圆O交于点E,连接AB交PO于点D.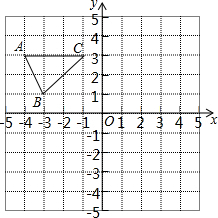 如图,已知△ABC的三个顶点坐标分别为A(-4,3),B(-3,1),C(-1,3).
如图,已知△ABC的三个顶点坐标分别为A(-4,3),B(-3,1),C(-1,3).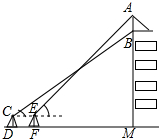 为了弘扬九十五中学办学理念,我校将“立己立人,尽善尽美”的校训印在旗帜上,放置在教学楼的顶部(如图所示).小华在教学楼前空地上的点D处,用1米高的测角仪CD,从点C测得旗帜的底部B的仰角为37°,然后向教学楼正方向走了4.8米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.若教学楼高BM=19米,且点A、B、M在同一直线上,求旗帜AB的高度(参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75.
为了弘扬九十五中学办学理念,我校将“立己立人,尽善尽美”的校训印在旗帜上,放置在教学楼的顶部(如图所示).小华在教学楼前空地上的点D处,用1米高的测角仪CD,从点C测得旗帜的底部B的仰角为37°,然后向教学楼正方向走了4.8米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.若教学楼高BM=19米,且点A、B、M在同一直线上,求旗帜AB的高度(参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75.