题目内容
9.在平面直角坐标系中,以A(2,4)为圆心,1为半径作⊙A,以B(3,5)为圆心,3为半径作⊙B,M、N分别是⊙A,⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为( )| A. | $\sqrt{82}$-4 | B. | $\sqrt{10}$-1 | C. | 6-2$\sqrt{2}$ | D. | $\sqrt{17}$-3 |
分析 作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,根据两点之间线段最短得到此时PM+PN最小,再利用对称确定A′的坐标,接着利用两点间的距离公式计算出A′B的长,然后用A′B的长减去两个圆的半径即可得到MN的长,即得到PM+PN的最小值.
解答  解:作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,
解:作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,
则此时PM+PN最小,
∵点A坐标(2,4),
∴点A′坐标(2,-4),
∵点B(3,5),
∴A′B=$\sqrt{(2-3)^{2}+(-4-5)^{2}}$=$\sqrt{82}$,
∴MN=A′B-BN-A′M=5 $\sqrt{82}$-3-1=$\sqrt{82}$-4,
∴PM+PN的最小值为 $\sqrt{82}$-4.
故选A
点评 本题考查了圆的综合题:掌握与圆有关的性质和关于x轴对称的点的坐标特征;会利用两点之间线段最短解决线段和的最小值问题;会运用两点间的距离公式计算线段的长;理解坐标与图形性质.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
19.已知10m=2,10n=3,则103m+2n=( )
| A. | 17 | B. | 72 | C. | 12 | D. | 36 |
17.在如图所示的某年12月份日历中,用长方形的方框圈出任意3×3个数.
(1)如果从左下角到右上角的“对角线”上的3个数字的和为54,那么这9个数的和为162,在这9个日期中,最后一天是26号;
(2)在这个月的日历中,用方框能否圈出“总和为171”的9个数?如果能,请求出这9个日期最后一天是几号;如果不能,请推测下个月的日历中,能否用方框圈出,如果能,请推测圈出的9个数中最后一天是星期几?
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
(2)在这个月的日历中,用方框能否圈出“总和为171”的9个数?如果能,请求出这9个日期最后一天是几号;如果不能,请推测下个月的日历中,能否用方框圈出,如果能,请推测圈出的9个数中最后一天是星期几?
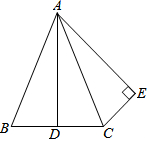 已知:如图,△ABC中,AB=AC,AD平分∠BAC,CE⊥AE于E,E在△ABC外,且CE=$\frac{1}{2}$BC.求证:∠ACE=∠B.
已知:如图,△ABC中,AB=AC,AD平分∠BAC,CE⊥AE于E,E在△ABC外,且CE=$\frac{1}{2}$BC.求证:∠ACE=∠B.