题目内容
1．若二次函数y=ax2+bx+c的x与y的部分对应值如下表：| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
| A． | 5 | B． | -3 | C． | -13 | D． | -27 |
分析 根据表格中的数据可以得到抛物线的对称轴，然后根据二次函数具有对称性，即可得到与x=0时对应的函数值．
解答 解：由表格可知，
二次函数y=ax2+bx+c的对称轴是直线x=$\frac{（-4）+（-2）}{2}$=-3，
∴当x=0时的函数值与x=-6时的函数值相等，
∴当x=0时，y的值为-13，
故选C．
点评 本题考查二次函数图象上点的坐标特征，解答本题的关键是明确二次函数的性质，求出二次函数的对称轴．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
4．下列运算正确的是（ ）
| A． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B． | ${（{-\frac{1}{2}x{y^2}}）^3}=-\frac{1}{6}{x^3}{y^6}$ | ||
| C． | （-x）5÷（-x）2=x3 | D． | $\sqrt{18}+\root{3}{-64}=3\sqrt{2}-4$ |
5．将二次函数y=x2+2x-1的图象沿x轴向右平移2个单位长度，得到的函数表达式是（ ）
| A． | y=（x+3）2-2 | B． | y=（x+3）2+2 | C． | y=（x-1）2+2 | D． | y=（x-1）2-2 |
2．已知圆锥的底面面积为9πcm2，母线长为6cm，则圆锥的侧面积是（ ）
| A． | 18πcm2 | B． | 27πcm2 | C． | 18cm2 | D． | 27cm2 |
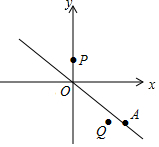如图，在平面直角坐标系中，点A是直线y=-x上一动点，点P的坐标为（0，1）点Q的坐标为（$\frac{3}{2}$，-2），当|AP-AQ|最大时，点A的坐标为（4，-4）．
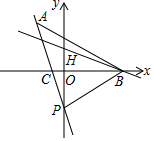如图，已知一次函数y=kx+b的图象经过点A（-2，5），并且与x轴交于点C，与y轴交于点P；直线y=-$\frac{1}{2}$x+3与x轴交于点B，与y轴交于点H，点H恰好与点P关于x轴对称．