题目内容
13.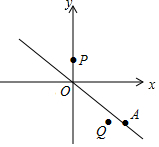 如图,在平面直角坐标系中,点A是直线y=-x上一动点,点P的坐标为(0,1)点Q的坐标为($\frac{3}{2}$,-2),当|AP-AQ|最大时,点A的坐标为(4,-4).
如图,在平面直角坐标系中,点A是直线y=-x上一动点,点P的坐标为(0,1)点Q的坐标为($\frac{3}{2}$,-2),当|AP-AQ|最大时,点A的坐标为(4,-4).
分析 先作点Q($\frac{3}{2}$,-2)关于直线y=-x对称的点Q'(2,-1.5),再连接AP,AQ,AQ',根据轴对称的性质可得AQ=AQ',根据|AP-AQ|≤PQ',可知当A,Q',P在同一直线上时,|AP-AQ|=PQ',此时|AP-AQ|有最大值,最后根据待定系数法求得直线解析式,并解方程组即可得到点A的坐标.
解答 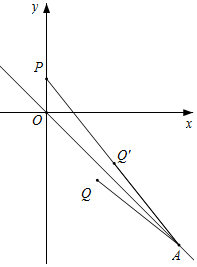 解:如图所示,作点Q($\frac{3}{2}$,-2)关于直线y=-x对称的点Q'(2,-1.5),
解:如图所示,作点Q($\frac{3}{2}$,-2)关于直线y=-x对称的点Q'(2,-1.5),
连接AP,AQ,AQ',则AQ=AQ',
由图可得,|AP-AQ|≤PQ',
∴当A,Q',P在同一直线上时,|AP-AQ|=PQ',
此时|AP-AQ|有最大值,
设直线PQ'的解析式为y=kx+b,
把(0,1),(2,-1.5)代入可得,
$\left\{\begin{array}{l}{-1.5=2k+b}\\{1=b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{5}{4}}\\{b=1}\end{array}\right.$,
∴直线PQ'的解析式为y=-$\frac{5}{4}$x+1,
解方程组$\left\{\begin{array}{l}{y=-\frac{5}{4}x+1}\\{y=-x}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=4}\\{y=-4}\end{array}\right.$,
∴A(4,-4),
故答案为:(4,-4).
点评 本题主要考查了一次函数图象上点的坐标特征以及最短路线问题,解决问题的关键是依据三角形的三边关系进行判断.凡是涉及最短距离的问题,一般要考虑线段的性质定理,多数情况要作点关于某直线的对称点.

| A. | 2.58×1011 | B. | 2.58×1012 | C. | 2.58×1013 | D. | 2.58×1014 |
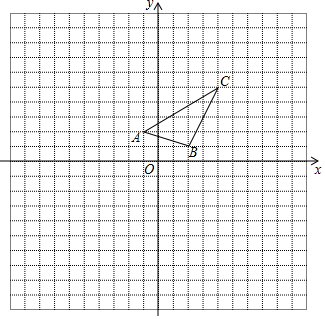 如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(-1,2)、B(2,1)、C(4,5).
如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(-1,2)、B(2,1)、C(4,5).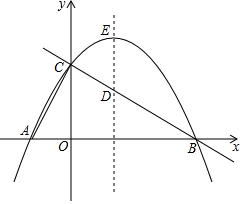 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{3}$x2+$\frac{2\sqrt{3}}{3}$x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{3}$x2+$\frac{2\sqrt{3}}{3}$x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E. 如图,已知抛物线y=-x2+2x+3与x轴分别交于A、B(点A在点B的左侧),与y轴交于点C,请问在直线BC下方的抛物线上是否存在点G,使得△BGC的面积为6?若存在,请求出点G的坐标;若不存在,请说明理由.
如图,已知抛物线y=-x2+2x+3与x轴分别交于A、B(点A在点B的左侧),与y轴交于点C,请问在直线BC下方的抛物线上是否存在点G,使得△BGC的面积为6?若存在,请求出点G的坐标;若不存在,请说明理由. 已知:一次函数y=kx+$\sqrt{3}$的图象如图所示,则k=$\frac{\sqrt{3}}{3}$.
已知:一次函数y=kx+$\sqrt{3}$的图象如图所示,则k=$\frac{\sqrt{3}}{3}$.