题目内容
13.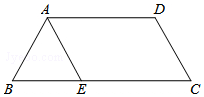 如图,在四边形ABCD中,AD∥BC,AB=CD=2,BC=5,∠BAD的平分线交BC于点E,且AE∥CD,试求四边形ABCD的面积.
如图,在四边形ABCD中,AD∥BC,AB=CD=2,BC=5,∠BAD的平分线交BC于点E,且AE∥CD,试求四边形ABCD的面积.
分析 根据题意可以判定△ABE是等边三角形,求得该三角形的高即为等腰梯形ABCD的高.所以利用梯形的面积公式进行解答.
解答 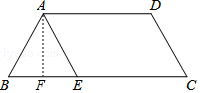 解:过点A作AF⊥BC于点F.
解:过点A作AF⊥BC于点F.
∵AD∥BC,
∴∠DAE=∠AEB,
又∵∠BAE=∠DAE,
∴∠BAE=∠AEB,
∵AE∥CD,
∴∠AEB=∠C,
∵AD∥BC,AB=CD=2,
∴四边形是等腰梯形,
∴∠B=∠C,
∴△ABE是等边三角形,
∴AB=AE=BE=2,∠B=60°,
∴AF=AB•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∵AD∥BC,AE∥CD,
∴四边形AECD是平行四边形,
∴AD=EC=BC-BE=5-2=3,…(4分)
∴梯形的面积=$\frac{1}{2}$(AD+BC)×AF=$\frac{1}{2}$×(3+5)×$\sqrt{3}$=4$\sqrt{3}$.
点评 本题考查了等边三角形的判定和性质,平行四边形的判定和性质,等腰梯形的性质等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.线段AB两端点坐标分别为A(-1,4),B(4,-2),现将线段AB平移后点A的对应点坐标为(-4,2),则点B的对应点的坐标为( )
| A. | (1,4) | B. | (1,-4) | C. | (2,-5) | D. | (1,0) |
3.点P(-3,-2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.某水果经销户用5200元从水果市场批发了苹果和桔子共700千克,苹果和桔子当天的批发价、零售价如下表:
(1)这天该经销户批发了苹果和桔子各多少千克?
(2)当天卖完这些苹果和桔子经销户能盈利多少元?
| 品名 | 苹果 | 桔子 |
| 批发价(元/千克) | 8.8 | 6.4 |
| 零售价(元/千克) | 14.4 | 10.4 |
(2)当天卖完这些苹果和桔子经销户能盈利多少元?
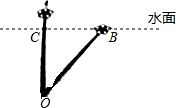 池塘中有一株荷花的茎长为OA,无风时露出水面部分CA=0.4米,如果把这株荷花旁边拉至使它的顶端A恰好到达池塘的水面B处,此时荷花顶端离原来位置的距离BC=1.2米,求这颗荷花的茎长OA.
池塘中有一株荷花的茎长为OA,无风时露出水面部分CA=0.4米,如果把这株荷花旁边拉至使它的顶端A恰好到达池塘的水面B处,此时荷花顶端离原来位置的距离BC=1.2米,求这颗荷花的茎长OA.