题目内容
2.线段AB两端点坐标分别为A(-1,4),B(4,-2),现将线段AB平移后点A的对应点坐标为(-4,2),则点B的对应点的坐标为( )| A. | (1,4) | B. | (1,-4) | C. | (2,-5) | D. | (1,0) |
分析 各对应点之间的关系是横坐标减3,纵坐标减2,那么让点B的横坐标减3,纵坐标减2即为点B的对应点的坐标.
解答 解:∵线段AB平移后点A(-1,4)的对应点坐标为(-4,2),
∴各对应点之间的关系是横坐标减3,纵坐标减2,
∵B(4,-2),
∴点B的对应点坐标为(4-3,-2-2),即(1,-4).
故选B.
点评 本题考查坐标与图形变化-平移;得到一对对应点的变换规律是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列等式一定成立的是( )
| A. | a2+a3=a5 | B. | (-x)9÷(-x)3=x6 | C. | (a-1)2=a2-1 | D. | (-2a2)3=8a6 |
13.如图中∠1与∠2不可能成为同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
10.不等式2x<-4的解集是( )
| A. | x>-2 | B. | x<-2 | C. | x>2 | D. | x<2 |
17.下列所给数中,是无理数的是( )
| A. | 2 | B. | $\frac{2}{7}$ | C. | 0.$\stackrel{•}{2}$ | D. | $\sqrt{2}$ |
7.下列各式中,不能与$\sqrt{\frac{1}{3}}$合并的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{1}{27}}$ | C. | $\sqrt{75}$ | D. | $\sqrt{0.3}$ |
14.若关于x的分式方程$\frac{2}{x-3}$+$\frac{x+m}{3-x}$=2无解,则m的值是( )
| A. | m=0或m=3 | B. | m=0 | C. | m=3 | D. | m=-1 |
11. 如图,桌面上一个一次性纸杯,它的左视图应是( )
如图,桌面上一个一次性纸杯,它的左视图应是( )
 如图,桌面上一个一次性纸杯,它的左视图应是( )
如图,桌面上一个一次性纸杯,它的左视图应是( )| A. |  | B. |  | C. |  | D. |  |
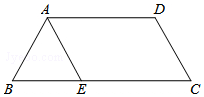 如图,在四边形ABCD中,AD∥BC,AB=CD=2,BC=5,∠BAD的平分线交BC于点E,且AE∥CD,试求四边形ABCD的面积.
如图,在四边形ABCD中,AD∥BC,AB=CD=2,BC=5,∠BAD的平分线交BC于点E,且AE∥CD,试求四边形ABCD的面积.