题目内容
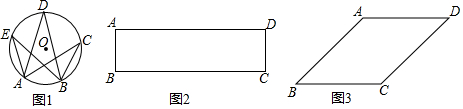
7.重温我们知道:同弧或等弧所对的圆周角相等.也就是,如图(1),⊙O中,$\widehat{AB}$所对的圆周角∠ACB=∠ADB=∠AEB.
应用
(1)已知:如图(2),矩形ABCD.
①若AB<$\frac{1}{2}$BC,在边AD上求作点P,使∠BPC=90°.(保留作图痕迹,写出作法.)
②小明经研究发现,当AB、BC的大小关系发生变化时,①中点P的个数也会发生变化,请你就点P的个数,探讨AB与BC之间的数量关系.(直接写出结论)
创新
(2)小明经进一步研究发现:命题“若四边形的一组对边相等和一组对角相等,则这个四边形是平行四边形.”是一个假命题,并在平行四边形的基础上利用“同弧或等弧所对的圆周角相等.”作出了一个反例图形.请你利用下面如图(3)所给的□ABCD作出该反例图形.(不写作法,保留作图痕迹)
分析 (1)①直接利用圆的性质得出BC的中点,进而得出⊙O,即可得出P点位置;
②利用①中所求,进而利用AB<$\frac{1}{2}$BC时,AB=$\frac{1}{2}$BC时,AB>$\frac{1}{2}$BC时,分别得出答案;
(2)利用圆周角定理结合圆的相关性质得出符合题意的图形.
解答  解:(1)①如图2所示:
解:(1)①如图2所示:
作法:以BC为直径作⊙O,交AD于P1、P2
P1、P2 为所求作的点P,
②AB<$\frac{1}{2}$BC时,点P有两个;
AB=$\frac{1}{2}$BC时,点P有且只有1个;
AB>$\frac{1}{2}$BC时,点P有0个;
(2)如图3所示:
连接AC,作△ADC的外接圆⊙O,再以C为圆心,CD的长为半径画弧,与⊙O相交于点E,则四边形ABCE即为所求反例图形.
点评 此题主要考查了圆的综合以及平行四边形的性质等知识,正确应用圆周角定理是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.当x=2时,代数式x2+ax+b的值是3;当x=-3时,这个代数式的值是-2,则2b-a的值是( )
| A. | -10 | B. | 10 | C. | 12 | D. | -12 |
15.若点P是第三象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是( )
| A. | (-4,-3) | B. | (4,-3) | C. | (-3,-4) | D. | (3,-4) |
2.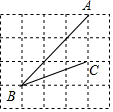 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
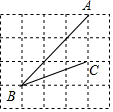 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
5.用-a表示的数一定是( )
| A. | 负数 | B. | 正数或负数 | C. | 负整数 | D. | 以上全不对 |
12.下列变形中错误的是( )
| A. | m2-(2m-n-p)=m2-2m+n+p | B. | m-n+p-q=m-(n+q-p) | ||
| C. | 3m-5n-1+2p=-(-3m)-[5n-(2p-1)] | D. | m+1-(-n+p)=-(-1+n-m+p) |
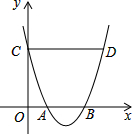 如图,抛物线y=ax2+bx+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,与抛物线交于点D,若OA=1,CD=4,则线段AB的长为( )
如图,抛物线y=ax2+bx+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,与抛物线交于点D,若OA=1,CD=4,则线段AB的长为( )