题目内容
2.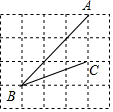 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
分析 根据题意,作CD⊥AB于点D,可以求得CD、BD的长,从而可以求出tan∠ABC的值.
解答  解:如图,作CD⊥AB于点D,则CD=$\sqrt{2}$,BD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
解:如图,作CD⊥AB于点D,则CD=$\sqrt{2}$,BD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
故tan∠ABC=$\frac{CD}{BD}$=$\frac{\sqrt{2}}{2\sqrt{2}}$=$\frac{1}{2}$.
故选B.
点评 本题考查的是勾股定理及解直角三角形,解题的关键是明确题意,构造直角三角形,利用锐角三角函数解答问题.

练习册系列答案
相关题目
12. 一个几何体的三视图如图所示,则该几何体表面积为( )
一个几何体的三视图如图所示,则该几何体表面积为( )
 一个几何体的三视图如图所示,则该几何体表面积为( )
一个几何体的三视图如图所示,则该几何体表面积为( )| A. | 3π | B. | 5π | C. | 6π | D. | 8π |
13.下列说法中,正确的个数有( )
①不带根号的数都是有理数;②无限小数都是无理数;
③任何实数都可以进行开立方运算;④$\frac{\sqrt{3}}{5}$不是分数.
①不带根号的数都是有理数;②无限小数都是无理数;
③任何实数都可以进行开立方运算;④$\frac{\sqrt{3}}{5}$不是分数.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
17.下列运算正确的是( )
| A. | (a-3)2=a2-9 | B. | a2•a4=a8 | C. | $\sqrt{9}$=±3 | D. | x6÷x3=x3 |
7.平面中2条不重合的直线至多可以将平面划分成4个区域,那么4条不重合的直线至多可以将平面划分成( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
5.下列方程组是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x-y=1}\\{xy=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{1}{x}-1=y}\\{3x+y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{{x}^{2}-x-2=0}\\{y=x+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{4x-y=-1}\\{y=2x+3}\end{array}\right.$ |
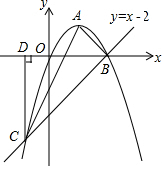 如图,已知抛物线y=-x2+2x的顶点为A,直线y=x-2与抛物线交于B,C两点.
如图,已知抛物线y=-x2+2x的顶点为A,直线y=x-2与抛物线交于B,C两点.