题目内容
6.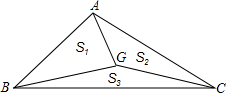 如图,G是△ABC的重心,其中△ABG、△ACG、△BCG的面积分别表示为S1、S2、S3,那么有( )
如图,G是△ABC的重心,其中△ABG、△ACG、△BCG的面积分别表示为S1、S2、S3,那么有( )| A. | S1=S2=S3 | B. | S1<S2<S3 | C. | S1=S2<S3 | D. | S1=S2>S3 |
分析 延长AG交BC于点D,则D是BC中点,过点B作BE⊥AG于E,过C作CF⊥AG于F,则易证△BDE≌△CDF,从而得出BE=CF,则△ABG与△ACG同底等高,面积相等,同理可证这三块面积两两相等,即三块面积相等.
解答 解:延长AG交BC于点D,则D是BC中点,过点B作BE⊥AG于E,过C作CF⊥AG于F,如图,
∵G是△ABC重心,
∴AD是△ABC中线,
∴BD=CD,
在△BDE和△CDF中,
$\left\{\begin{array}{l}{BD=CD}\\{∠BDE=∠CDF}\\{∠BED=∠CFD}\end{array}\right.$,
∴△BDE≌△CDF(AAS),
∴BE=CF,
∴${S}_{1}=\frac{1}{2}×AG×BE=\frac{1}{2}×AG×CF$=S2,
同理可证:S2=S3,
∴S1=S2=S3.
点评 本题主要考查重心的定义和性质.只要明白重心就是三条中线的交点,那么问题就变得简单.事实上,由共边定理是可以直接得结论的,或者说由小学奥数中燕尾定理也是可以直接得结论的.对于不知道这些内容的同学就按照这里所给出的证明方法理解.

练习册系列答案
相关题目
17.在-(-9),(-1)2013,-33,-|-2|中,负数共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,若DE∥FG∥BC,AD=DF=FB,则两个三角形面积比S△ADE:S△ABC=1:9.
如图,若DE∥FG∥BC,AD=DF=FB,则两个三角形面积比S△ADE:S△ABC=1:9. 在平面直角坐标系中,O为坐标原点,抛物线y=-x2+kx+4与y轴交于A,与x轴的负半轴交于B,且△ABO的面积是8.
在平面直角坐标系中,O为坐标原点,抛物线y=-x2+kx+4与y轴交于A,与x轴的负半轴交于B,且△ABO的面积是8.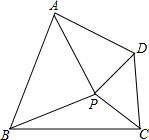 P为四边形ABCD内一点,如果△PAB和△PCD都是以AB,CD为底的等腰直角三角形,则该四边形称为“对底四边形”,AB,CD叫底.
P为四边形ABCD内一点,如果△PAB和△PCD都是以AB,CD为底的等腰直角三角形,则该四边形称为“对底四边形”,AB,CD叫底.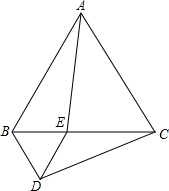 如图,等边三角形ABC的边长为4,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD.
如图,等边三角形ABC的边长为4,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD.