题目内容
 如图,∠AOB=30°,⊙M的圆心在OA上,半径为4cm,若圆心在射线OA上移动,则当OM=
如图,∠AOB=30°,⊙M的圆心在OA上,半径为4cm,若圆心在射线OA上移动,则当OM=考点:切线的判定
专题:
分析:当OB与⊙M相切时,设切点为C,连接MC,则可求得MC=4,在Rt△OMC中可求得OM.
解答: 解:
解:
设OB与⊙M相切于点C,连接MC,则MC⊥OB,且MC=4cm,
∵∠AOB=30°,
∴OM=2MC=8cm,
故答案为:8.
 解:
解:设OB与⊙M相切于点C,连接MC,则MC⊥OB,且MC=4cm,
∵∠AOB=30°,
∴OM=2MC=8cm,
故答案为:8.
点评:本题主要考查切线的性质,掌握过切点的半径与切线垂直是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
绝对值不大于4的所有整数的和是( )
| A、16 | B、0 | C、576 | D、-1 |
 如图,在半径为10的⊙O中,AB、CD是互相垂直的两条相等的弦,垂足为P,若OP=6
如图,在半径为10的⊙O中,AB、CD是互相垂直的两条相等的弦,垂足为P,若OP=6| 2 |
| A、12 | B、14 | C、16 | D、18 |
 如图,∠AOB是直角,∠BOC=50°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为
如图,∠AOB是直角,∠BOC=50°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为 如图,已知点A、O、B在同一条直线上,∠AOC=∠BOC=EOF=90°,则∠COE的余角有
如图,已知点A、O、B在同一条直线上,∠AOC=∠BOC=EOF=90°,则∠COE的余角有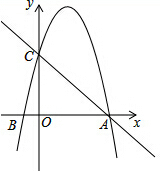 如图,抛物线y=-x2+3x+4的图象交x轴于A,B,交y轴于C,点P是抛物线的一点,若以△ACP是以AC为直角边的直角三角形,求点P的坐标.
如图,抛物线y=-x2+3x+4的图象交x轴于A,B,交y轴于C,点P是抛物线的一点,若以△ACP是以AC为直角边的直角三角形,求点P的坐标.