题目内容
解方程：y2=62+（4+x）2，其中6：y=4：x．
考点：换元法解一元二次方程
专题：
分析：首先将已知代入得出y=
x，进而利用因式分解法解方程，进而得出答案．
| 3 |
| 2 |
解答：解：∵6：y=4：x，
∴y=
x，
∴y2-（4+x）2-36=0，
∴5x2-32x-208=0
（x+4）（5x-52）=0，
解得：x1=-4，x2=
，
故
，
．
∴y=
| 3 |
| 2 |
∴y2-（4+x）2-36=0，
∴5x2-32x-208=0
（x+4）（5x-52）=0，
解得：x1=-4，x2=
| 52 |
| 5 |
故
|
|
点评：此题主要考查了换元法解一元二次方程，正确消元得出是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
在
，3.33，
，-2
，0.454455444555…，
，-
，127中，无理数的个数有（ ）
| 7 |
| 22 |
| π |
| 2 |
| 1 |
| 2 |
|
| 0.9 |
| A、2个 | B、3个 | C、4个 | D、5个 |
已知a2-2a-3=0，则a2-2a-
的值为（ ）
| 1 |
| 2a2-4a |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
如图，∠AOB=30°，⊙M的圆心在OA上，半径为4cm，若圆心在射线OA上移动，则当OM=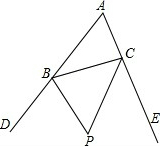
如图，在△ABC中，BP、CP分别是△ABC的外角∠DBC和∠ECB的平分线．
如图所示，在Rt△ABC中，∠C=90°，AC=5，BC=3，求AB和sinA．