题目内容
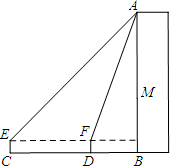 黄冈市高效课堂现场会在英山实验中学召开,为营造氛围,举办方从教学楼顶端A点处向下悬挂“优化教学方法,构建高效课堂”大型标语.九年级学生王港用高1m的测角仪在地面C点测得楼顶A点的仰角为45°,沿CB方向前进15m到达D点,测得A点仰角的正切值为
黄冈市高效课堂现场会在英山实验中学召开,为营造氛围,举办方从教学楼顶端A点处向下悬挂“优化教学方法,构建高效课堂”大型标语.九年级学生王港用高1m的测角仪在地面C点测得楼顶A点的仰角为45°,沿CB方向前进15m到达D点,测得A点仰角的正切值为| 8 |
| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:应用题
分析:设AG=x,在Rt△AEG中求出EG,在Rt△AFG中求出FG,根据EF=15m,可建立方程,求出x的值后即可计算标语AM的长度.
解答:解:设AG=x,
由题意得,∠AEG=45°,tan∠AFG=
,
在Rt△AEG中,EG=
=
=x,
在Rt△AFG中,FG=
=
x,
∵EF=15m,
∴x-
x=15,
解得:x=24,即AG=24米,
∵标语底端M点距地面9m,
∴标语AM的长度=AG+GB-9=16米.
答:标语AM的长度为16米.

由题意得,∠AEG=45°,tan∠AFG=
| 8 |
| 3 |
在Rt△AEG中,EG=
| AG |
| tan∠AEG |
| AG |
| tan45° |
在Rt△AFG中,FG=
| AG |
| tan∠AFG |
| 3 |
| 8 |
∵EF=15m,
∴x-
| 3 |
| 8 |
解得:x=24,即AG=24米,
∵标语底端M点距地面9m,
∴标语AM的长度=AG+GB-9=16米.
答:标语AM的长度为16米.

点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数的知识表示出相关线段的长度,难度一般.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列计算正确的是( )
| A、a+a=a2 |
| B、a3•a5=a8 |
| C、(a3)4=a7 |
| D、(-a-b)(b-a)=b2-a2 |
袋子里有黑球、红球和白球共1000个,为了了解各色球的个数,小刚经过实验了解到随机摸出一个是黑球的概率是
,是红球的概率是
,那么白球的个数是( )
| 7 |
| 20 |
| 13 |
| 50 |
| A、350 | B、260 |
| C、390 | D、510 |
 如图,在矩形ABCD中,AB=10cm,BC=4cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D停止,当运动时间为
如图,在矩形ABCD中,AB=10cm,BC=4cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D停止,当运动时间为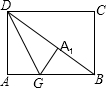 如图,在矩形纸片ABCD中,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,折痕为DG,点A落在点A1处,则AG的长为( )
如图,在矩形纸片ABCD中,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,折痕为DG,点A落在点A1处,则AG的长为( )