题目内容
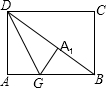 如图,在矩形纸片ABCD中,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,折痕为DG,点A落在点A1处,则AG的长为( )
如图,在矩形纸片ABCD中,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,折痕为DG,点A落在点A1处,则AG的长为( )| A、2 | B、3 | C、4 | D、5 |
考点:翻折变换(折叠问题)
专题:
分析:根据勾股定理可得BD=10,由折叠的性质可得△ADG≌△A1DG,则A1D=AD=6,A1G=AG,则A1B=10-6=4,在Rt△A1BG中根据勾股定理求AG的即可.
解答:解:在Rt△ABD中,AB=8,AD=6,
则BD=
=
=10,
由折叠的性质可得:△ADG≌△A1DG,
∴A1D=AD=6,A1G=AG,
∴A1B=10-6=4,
设AG=x,则:A1G=AG=x,BG=8-x,
在Rt△A1BG中,x2+42=(8-x)2
解得:x=3,
即AG长为3.
故选B.
则BD=
| AB2+AD2 |
| 82+62 |
由折叠的性质可得:△ADG≌△A1DG,
∴A1D=AD=6,A1G=AG,
∴A1B=10-6=4,
设AG=x,则:A1G=AG=x,BG=8-x,
在Rt△A1BG中,x2+42=(8-x)2
解得:x=3,
即AG长为3.
故选B.
点评:此题主要考查折叠的性质,综合利用了勾股定理的知识,认真分析图中各条线段的关系是解题的关键,难度一般.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
因式分解-2a2+8ab-8b2结果正确的是( )
| A、-2(a2-4ab+4b2) |
| B、-2(a-2b)2 |
| C、-2(a+2b)2 |
| D、2(a-2b)2 |
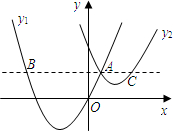 如图,抛物线y1=a(x+2)2+c与y2=
如图,抛物线y1=a(x+2)2+c与y2=| 1 |
| 2 |
| A、c=4a |
| B、a=1 |
| C、当x=0时,y2-y1=4 |
| D、2AB=3AC |
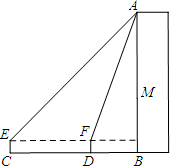 黄冈市高效课堂现场会在英山实验中学召开,为营造氛围,举办方从教学楼顶端A点处向下悬挂“优化教学方法,构建高效课堂”大型标语.九年级学生王港用高1m的测角仪在地面C点测得楼顶A点的仰角为45°,沿CB方向前进15m到达D点,测得A点仰角的正切值为
黄冈市高效课堂现场会在英山实验中学召开,为营造氛围,举办方从教学楼顶端A点处向下悬挂“优化教学方法,构建高效课堂”大型标语.九年级学生王港用高1m的测角仪在地面C点测得楼顶A点的仰角为45°,沿CB方向前进15m到达D点,测得A点仰角的正切值为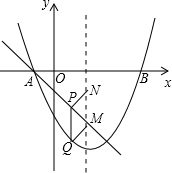 如图,抛物线y=ax2+bx-
如图,抛物线y=ax2+bx-