题目内容
如图，OC=OD，BC=AD，求证：∠A=∠B．考点：全等三角形的判定与性质
专题：证明题
分析：先求出OA=OB，然后利用“边角边”证明△OAC和△OBD全等，再根据全等三角形对应角相等即可得证．
解答：证明：∵OC=OD，BC=AD，
∴OC+BC=OD+AD，
即OA=OB，
在△OAC和△OBD中，
，
∴△OAC≌△OBD（SAS），
∴∠A=∠B．
∴OC+BC=OD+AD，
即OA=OB，
在△OAC和△OBD中，
|
∴△OAC≌△OBD（SAS），
∴∠A=∠B．
点评：本题考查了全等三角形的判定与性质，是基础题，求出OA=OB是解题的关键．
练习册系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
如图，已知点A的坐标为（| 3 |
| k |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
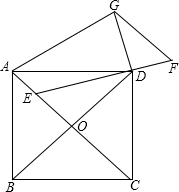如图，正方形ABCD中，对角线AC与BD相交于O，∠ADE=15°，过D作DG⊥ED于D，且AG=AD，过G作GF∥AC交ED的延长线于F．
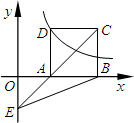如图，在平面直角坐标系中，正方形ABCD的顶点A、B在x轴正半轴上，顶点D在反比例函数
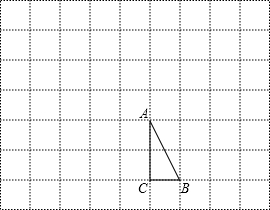如图在7×9的小正方形网格中，△ABC的顶点A、B、C在网格的格点上，将△ABC向左平移3个单位，再向上平移3个单位得到△A′B′C′，将△ABC按一定规律顺次旋转，第1次将△ABC绕点B顺时针旋转90°得到△A1BC1，第2次将△A1BC1绕点A1顺时针旋转90°得到△A1BC2，第3次将△A1BC2绕点C2顺时针旋转90°得到△A2B2C2，第4次将△A2B2C2绕点B2顺时针旋转90°得到△A3B2C3，依次旋转下去．
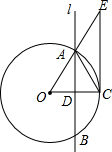如图，直线l与⊙O交于A，B两点，且与半径OC垂直，垂足为点D，连接AC，在线段OA的延长线上取一点E，使AE=AC，连接CE．已知OA=4，∠O=60°
如图，量一量，算一算．