题目内容
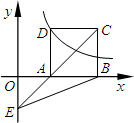 如图,在平面直角坐标系中,正方形ABCD的顶点A、B在x轴正半轴上,顶点D在反比例函数y=
如图,在平面直角坐标系中,正方形ABCD的顶点A、B在x轴正半轴上,顶点D在反比例函数y=| k |
| x |
考点:反比例函数综合题
专题:压轴题
分析:设正方形ABCD的边长为a,A(x,0),则D(x,a),再由点D在反比例函数y=
的图象上可知,k=xa,根据正方形的性质得出∠CAB的度数,根据对顶角相等可得出∠OAE的度数,进而判断出△OAE的形状,故可得出E点坐标,根据△ABE的面积为1.5即可得出k的值.
| k |
| x |
解答:解:设正方形ABCD的边长为a,A(x,0),则D(x,a),
∵点D在反比例函数y=
的图象上,
∴k=xa,
∵四边形ABCD是正方形,
∴∠CAB=45°,
∴∠OAE=∠CAB=45°,
∴△OAE是等腰直角三角形,
∴E(0,-x),
∴S△ABE=
AB•OE=
ax=1.5,
∴ax=3,即k=3.
故答案为:3.
∵点D在反比例函数y=
| k |
| x |
∴k=xa,
∵四边形ABCD是正方形,
∴∠CAB=45°,
∴∠OAE=∠CAB=45°,
∴△OAE是等腰直角三角形,
∴E(0,-x),
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∴ax=3,即k=3.
故答案为:3.
点评:本题考查的是反比例函数综合题,涉及到正方形的性质及反比例函数图象上点的坐标特点等相关知识,难度适中.

练习册系列答案
相关题目
不等式组
的解集,在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
在数轴上表示不等式组
的解集正确的是( )
|
A、 |
B、 |
C、 |
D、 |
一只草履虫每小时大约能形成60个食物泡,每个食物泡大约含有30个细菌,因此,一只草履虫每天大约能吞噬43000个细菌,将43000用科学记数法科表示为( )
| A、43×103 |
| B、4.3×104 |
| C、0.43×105 |
| D、4.3×105 |
 如图,OC=OD,BC=AD,求证:∠A=∠B.
如图,OC=OD,BC=AD,求证:∠A=∠B. 如图,在由边长为1的小正方形组成的网格中,△ABC的顶点均落在格点上
如图,在由边长为1的小正方形组成的网格中,△ABC的顶点均落在格点上 如图,直线AB与直线CD相交于点O,射线OP平分∠AOD,若∠BOC=130°,则∠COP的度数为
如图,直线AB与直线CD相交于点O,射线OP平分∠AOD,若∠BOC=130°,则∠COP的度数为