题目内容
17.老师给出一个二次函数,甲,乙,丙三位同学各指出这个函数的一个性质:甲:函数的图象经过第一、二、四象限;
乙:当x<2时,y随x的增大而减小,当x>2时,y随x的增大而减大;
丙:函数的图象与坐标轴只有两个交点;
已知这三位同学叙述都正确,请构造出满足上述所有性质的一个函数y=(x-2)2-3.
分析 利用二次函数的性质可判断抛物线开口向上,抛物线与y轴的交点在x轴上方,于是可设a=1,c=1,再利用二次函数的确定抛物线的对称轴为直线x=2,然后利用函数的图象与坐标轴只有两个交点得到抛物线的顶点坐标为(2,0),再设顶点式求抛物线解析式.
解答 解:由函数的图象经过第一、二、四象限可判断抛物线开口向上,抛物线与y轴的交点在x轴上方,可设a=1,c=1,
因为当x<2时,y随x的增大而减小,当x>2时,y随x的增大而减大,则抛物线的对称轴为直线x=2,
由函数的图象与坐标轴只有两个交点,则抛物线的顶点坐标为(2,0),
所以抛物线解析式为y=(x-2)2+m,
把(0,1)代入得1=4+m,解得m=-3,
即抛物线解析式为y=(x-2)2-3.
故答案为y=(x-2)2-3.
点评 本题考查了二次函数的性质:熟练掌握二次函数的性质是解决此题的关键.

练习册系列答案
相关题目
18.某天的温度上升-2℃的意义是( )
| A. | 上升了2℃ | B. | 下降了-2℃ | C. | 下降了2℃ | D. | 没有变化 |
 如图,菱形ABCD中,BP=CP,MN∥AB,求证:
如图,菱形ABCD中,BP=CP,MN∥AB,求证: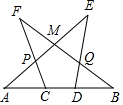 如图,A、C、D、B四点共线,AC=BD,∠A=∠B,∠E=∠F,图中全等三角形有( )对.
如图,A、C、D、B四点共线,AC=BD,∠A=∠B,∠E=∠F,图中全等三角形有( )对. 如图,∠A+∠B+∠C+∠D+∠E+∠F=360°.
如图,∠A+∠B+∠C+∠D+∠E+∠F=360°. 如图,函数y=-2x与y=$\frac{k}{x}$的图象相交于A(m,2)、B两点.
如图,函数y=-2x与y=$\frac{k}{x}$的图象相交于A(m,2)、B两点.