题目内容
15.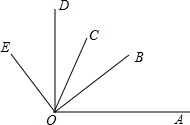 如图,OB是∠AOC的平分线,OD是∠COE的平分线.
如图,OB是∠AOC的平分线,OD是∠COE的平分线.(1)如果∠AOE=142°,∠EOC=40°,求∠BOC的度数;
(2)如果∠AOE=142°,求∠BOD的度数;
(3)直接写出∠AOE与∠BOD之间的数量关系.
分析 (1)角平分线的定义求得∠BOC=51°;
(2)角平分线的定义求得∠BOD=71°;
(3)根据角平分线的定义易求∠AOE=2∠BOD.
解答 解:(1)OB是∠AOC的平分线,
∴∠BOC=$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(∠AOE-EOC)
=$\frac{1}{2}$(1420-400)=51°,
(2)OD是∠COE的平分线
∠BOD=∠BOC+∠COD
=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠COE
=$\frac{1}{2}$(∠AOC+∠COE).
=$\frac{1}{2}$∠AOE=$\frac{1}{2}$×1420=71°
(3)因为OB是∠AOC的平分线,
所以 AOC=2∠BOC.
因为OD是∠EOC的平分线,
所以 COE=2∠COD.
所以∠AOE=∠AOC+∠COE
=2∠BOC+2∠COD
=2∠BOD
点评 本题考查了角平分线的定义.解题时,实际上是根据角平分线定义得出所求角与已知角的关系转化求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知OA=OC,OB=OD,∠AOC=∠BOD,求证:∠A=∠C.
如图,已知OA=OC,OB=OD,∠AOC=∠BOD,求证:∠A=∠C.
 已知:线段a、c.
已知:线段a、c. 如图,在△ABC中,∠C=90°,DM⊥AB于点M,DN⊥BC于点N,交AB于点E.
如图,在△ABC中,∠C=90°,DM⊥AB于点M,DN⊥BC于点N,交AB于点E. 如图,点B、E、F、C在同一条直线上,且AB=DE,BE=CF.
如图,点B、E、F、C在同一条直线上,且AB=DE,BE=CF. 如图,AB=BC,BD=EC,AB⊥BC,EC⊥BC,求证:AD⊥BE.
如图,AB=BC,BD=EC,AB⊥BC,EC⊥BC,求证:AD⊥BE.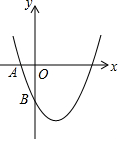 如图,函数y=x2-2x-3与坐标轴交于A、B两点,问抛物线上是否存在点C使四边形ABCO为平行四边形,若存在,求出点C的坐标;若不存在,说明理由.
如图,函数y=x2-2x-3与坐标轴交于A、B两点,问抛物线上是否存在点C使四边形ABCO为平行四边形,若存在,求出点C的坐标;若不存在,说明理由.