题目内容
8. 如图,⊙O的外切正方形ABCD的边长为2cm,求⊙O的内接正六边形的面积.
如图,⊙O的外切正方形ABCD的边长为2cm,求⊙O的内接正六边形的面积.
分析 过点O作OH⊥AD于点H,交EF于点G,根据正方形ABCD的边长为2cm可得出OH=1cm,根据正六边形的性质得出∠EOF的度数,由垂径定理可知∠EOG的度数及EF=2EG,根据直角三角形的性质得出EF及OG的长,进而可得出结论.
解答 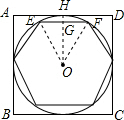 解:如图,过点O作OH⊥AD于点H,交EF于点G,
解:如图,过点O作OH⊥AD于点H,交EF于点G,
∵正方形ABCD的边长为2cm,
∴OH=1cm.
∵图中是正六边形,
∴∠EOF=60°.
∵OG⊥EF,
∴∠EOG=30°,EF=2EG,
∵OE=OH=1cm,
∴OG=OE•ctan30°=1×$\sqrt{3}$=$\sqrt{3}$cm,EF=OE=1cm,
∴⊙O的内接正六边形的面积=6S△EOF=6×$\frac{1}{2}$×1×$\sqrt{3}$=3$\sqrt{3}$(cm2).
答:⊙O的内接正六边形的面积为3$\sqrt{3}$cm2.
点评 本题考查的是正多边形和圆,熟知正方形及正六边形的性质是解答此题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目