题目内容
(1)当a=| 2 |
| 2a+2 |
| a2+2a-3 |
| 1 |
| a+3 |
(2)解不等式组并写出其整数解:
|
分析:(1)首先将分式的分子与分母进行因式分解,再通分化简,整理后代入a的值即可求出;
(2)分别解不等式,得出不等式组的解集,即可得出整数解.
(2)分别解不等式,得出不等式组的解集,即可得出整数解.
解答:解:(1)
-
,
=
-
,
=
,
当a=
时,原式=
=
+1;
(2)
,
解:解不等式3(x+1)>4x+2,
解得:x<1,
解不等式
≥
,
解得:x≥-2,
∴不等式组的解集为:-2≤x<1,
∴其整数解为:-2,-1,0.
| 2a+2 |
| a2+2a-3 |
| 1 |
| a+3 |
=
| 2(a+1) |
| (a-1)(a+3) |
| a-1 |
| (a-1)(a+3) |
=
| 1 |
| a-1 |
当a=
| 2 |
| 1 | ||
|
| 2 |
(2)
|
解:解不等式3(x+1)>4x+2,
解得:x<1,
解不等式
| x |
| 2 |
| x-1 |
| 3 |
解得:x≥-2,
∴不等式组的解集为:-2≤x<1,
∴其整数解为:-2,-1,0.
点评:此题主要考查了不等式组的解法以及分式的混合运算,两种题型都是初中阶段重点题型也是中考中考查重点,计算时应特别注意.

练习册系列答案
相关题目
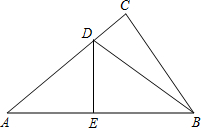 如图,在△ABC中,∠ACB=90°,若把△ABC沿直线DE折叠,使△ADE与△BDE重合.
如图,在△ABC中,∠ACB=90°,若把△ABC沿直线DE折叠,使△ADE与△BDE重合.