题目内容
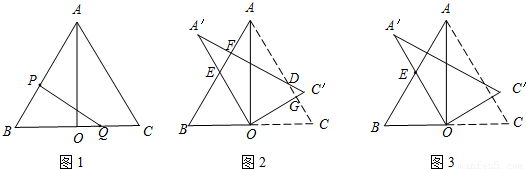
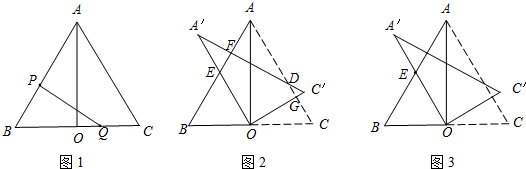
把两块完全一样的三角板如图1放置,其中∠BAO=∠CAO=30°,∠ABO=∠ACO=60°,B、O、C三点在同一条直线上,斜边AB=AC=6cm,动点P由B出发,沿折线B→A→C以每秒2cm的速度向C运动,同时动点Q从C出发以每秒
cm的速度向点B运动,当其中一个点到达终点时,另一个点也停止运动,设运动时间为t秒.
(1)设△BPQ的面积为S,求S与t之间的函数关系式,并写出自变量的取值范围;
(2)如图2,把△OCA绕点O逆时针旋转,旋转后得到△OC′A′,当∠COC′=∠CAO 时,求△OC′A′与△ABC重叠部分的面积;
(3)如图3,在△OCA绕点O逆时针旋转的过程中(0°<旋转角<180°),设A′O所在直线与BA所在直线交点为E,是否存在点E使得△OAE为等腰三角形?若存在,直接写出线段OE的长;若不存在,请说明理由.
| 3 |
(1)设△BPQ的面积为S,求S与t之间的函数关系式,并写出自变量的取值范围;
(2)如图2,把△OCA绕点O逆时针旋转,旋转后得到△OC′A′,当∠COC′=∠CAO 时,求△OC′A′与△ABC重叠部分的面积;
(3)如图3,在△OCA绕点O逆时针旋转的过程中(0°<旋转角<180°),设A′O所在直线与BA所在直线交点为E,是否存在点E使得△OAE为等腰三角形?若存在,直接写出线段OE的长;若不存在,请说明理由.

分析:(1)根据三角形的面积公式S△BOQ=BP•BQ•sinB即可求解;
(2)可以证得△根据S重叠=S△OAB-S△OBE-S△ADF,利用三角形的面积公式即可求解;
(3)分A是顶角顶点,则AE=OA,则E可能在线段AB上,也可能在BA的延长线上,利用三角函数即可求得OE的长度;
当E是顶角的顶点时,AE=OE,在△AOE中,∠EAO=30°,则利用三角函数即可求得OE的长;
当O是顶角的顶点时,E在AB的延长线上,利用三角函数即可求得OE的长.
(2)可以证得△根据S重叠=S△OAB-S△OBE-S△ADF,利用三角形的面积公式即可求解;
(3)分A是顶角顶点,则AE=OA,则E可能在线段AB上,也可能在BA的延长线上,利用三角函数即可求得OE的长度;
当E是顶角的顶点时,AE=OE,在△AOE中,∠EAO=30°,则利用三角函数即可求得OE的长;
当O是顶角的顶点时,E在AB的延长线上,利用三角函数即可求得OE的长.
解答:解:(1)当0<t≤3时,S=
(6-
t)×
t=-
t2+3
t.
当3<t<2
时,S=
(6-
t)•
(12-2t)=
t2-(3
+9)t+18
;
(2)S重叠=S△OAB-S△OBE-S△ADF=
×3×3
-
×3×
-
×
×
=
;
(3)在直角△AOB中,OA=AB•cos∠BAO=6×
=3
,
1)当A是顶角顶点时,AE=OA=3
,
分两种情况,当E在线段AB上时,OE=
=
,
当E在射线BA上时,OE=
=
;
2)当E是等腰三角形的顶角的顶点时,OE=AE=
=
=3;
3)当O是等腰三角形的顶角顶点时,此时E在线段AB的延长线上,OE=OA=3
cm,
总之,存在点E,使得△OAE是等腰三角形,线段OE的长分别是:3或3
或
或
.
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
当3<t<2
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
(2)S重叠=S△OAB-S△OBE-S△ADF=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
3
| ||
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
9-3
| ||
| 2 |
27-9
| ||
| 4 |
(3)在直角△AOB中,OA=AB•cos∠BAO=6×
| ||
| 2 |
| 3 |
1)当A是顶角顶点时,AE=OA=3
| 3 |
分两种情况,当E在线段AB上时,OE=
| AE2+OA2-2AE•OA•cos30° |
9
| ||||
| 2 |
当E在射线BA上时,OE=
| AE2+OA2+2AE•OA•cos30° |
9
| ||||
| 2 |
2)当E是等腰三角形的顶角的顶点时,OE=AE=
| ||
| cos30° |
| ||||
|
3)当O是等腰三角形的顶角顶点时,此时E在线段AB的延长线上,OE=OA=3
| 3 |
总之,存在点E,使得△OAE是等腰三角形,线段OE的长分别是:3或3
| 3 |
9
| ||||
| 2 |
9
| ||||
| 2 |
点评:本题考查了三角形的面积公式,以及三角函数,等腰三角形的性质,正确进行讨论是关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
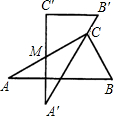 角顶点,如图所示,∠A=30°,AC=10,则此时两直角顶点C,C′间的距离是
角顶点,如图所示,∠A=30°,AC=10,则此时两直角顶点C,C′间的距离是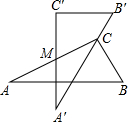 (2011•太原二模)如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=2,则这块直角三角板顶点A、A′之间的距离等于
(2011•太原二模)如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=2,则这块直角三角板顶点A、A′之间的距离等于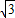 cm的速度向点B运动,当其中一个点到达终点时,另一个点也停止运动,设运动时间为t秒.
cm的速度向点B运动,当其中一个点到达终点时,另一个点也停止运动,设运动时间为t秒.