题目内容
15.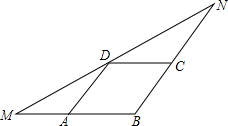 如图,在△MBN中,BM=6,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则?ABCD的周长是( )
如图,在△MBN中,BM=6,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则?ABCD的周长是( )| A. | 24 | B. | 18 | C. | 16 | D. | 12 |
分析 首先根据平行四边形的性质可得AB∥DC,AD∥BN,根据平行线的性质可得∠N=∠ADM,∠M=∠NDC,再由∠NDC=∠MDA,可得∠N=∠NDC,∠M=∠MDA,∠M=∠N,根据等角对等边可得CN=DC,AD=MA,NB=MB,进而得到答案.
解答 解:∵四边形ABCD为平行四边形,
∴AD=BC,DC=AB,AB∥DC,AD∥BN,
∴∠N=∠ADM,∠M=∠NDC,
∵∠NDC=∠MDA,
∴∠N=∠NDC,∠M=∠MDA,∠M=∠N,
∴CN=DC,AD=MA,NB=MB,
∴平行四边形ABCD的周长是 BM+BN=6+6=12,
故答案为:12.
点评 此题主要考查了平行四边形的性质,关键是掌握平行四边形对边相等.

练习册系列答案
相关题目
5.当分式$\frac{x-1}{x+2}$的值为0时,x的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
6.计算:($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)=( )
| A. | 5+2$\sqrt{6}$ | B. | 1 | C. | 5-2$\sqrt{6}$ | D. | 5 |
4. 将如图所示的正方体沿某些棱展开后( )
将如图所示的正方体沿某些棱展开后( )
 将如图所示的正方体沿某些棱展开后( )
将如图所示的正方体沿某些棱展开后( )| A. |  | B. |  | C. |  | D. |  |
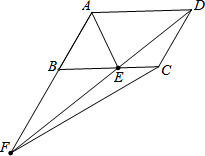 如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=2cm,则△CEF面积是$\sqrt{3}$cm2.
如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=2cm,则△CEF面积是$\sqrt{3}$cm2.
 如图:点C,D分别表示两所大学,AO,BO表示两条公路,现计划修建一个超市,希望超市到两所大学的距离相等,到两条公路的距离也相等,请你找出超市所在的位置.(只用直尺和圆规)
如图:点C,D分别表示两所大学,AO,BO表示两条公路,现计划修建一个超市,希望超市到两所大学的距离相等,到两条公路的距离也相等,请你找出超市所在的位置.(只用直尺和圆规)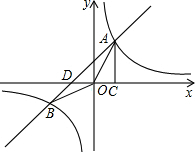 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+1的图象相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+1的图象相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,