题目内容
17.一次函数图象经过A(-2,0)与y轴交于点B,若△AOB面积为6,求这个函数解析式.分析 设函数解析式为y=kx+b,则B(0,b),利用三角形面积公式得到$\frac{1}{2}$•2•|b|=6,解得b=3或b=-3,然后把A(-2,0),b=3或A(-2,0),b=-3代入y=kx+b中求出对应的k的值,从而得到一次函数解析式.
解答 解:设函数解析式为y=kx+b,则B(0,b),
根据题意得$\frac{1}{2}$•2•|b|=6,解得b=3或b=-3,
把A(-2,0),b=3代入y=kx+b得-2k+3=0,解得k=$\frac{3}{2}$,此时函数解析式为y=$\frac{3}{2}$x+3;
把A(-2,0),b=-3代入y=kx+b得-2k-3=0,解得k=-$\frac{3}{2}$,此时函数解析式为y=-$\frac{3}{2}$x-3.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
5.当分式$\frac{x-1}{x+2}$的值为0时,x的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
12.点(-2,5)关于x轴对称的点的坐标是( )
| A. | (2,-5) | B. | (-2,-5) | C. | (2,5) | D. | (5,-2) |
9.下列运算正确的是( )
| A. | a6÷a2=a4 | B. | a3+a3=a6 | C. | (-2x)3=-6x3 | D. | a3•a3=a9 |
6.计算:($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)=( )
| A. | 5+2$\sqrt{6}$ | B. | 1 | C. | 5-2$\sqrt{6}$ | D. | 5 |
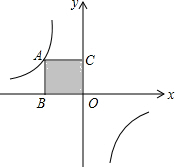 如图,正方形ABOC的面积为4,反比例函数y=$\frac{k}{x}$的图象过点A,则k=-4.
如图,正方形ABOC的面积为4,反比例函数y=$\frac{k}{x}$的图象过点A,则k=-4.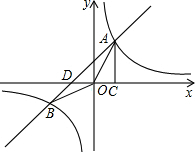 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+1的图象相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+1的图象相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,