题目内容
8.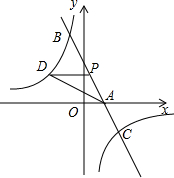 如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5),C($\frac{5}{2}$,d)两点,点M是y轴上一动点,点P(m,n)是一次函数y=kx+b的图象上的动点.
如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5),C($\frac{5}{2}$,d)两点,点M是y轴上一动点,点P(m,n)是一次函数y=kx+b的图象上的动点.(1)求k、b的值;
(2)当MA+MC的值最小时,求点M的坐标;
(3)设-1$<m<\frac{3}{2}$,过点P作x轴的平行线与函数y2=$\frac{c}{x}$的图象相交于点D.试问△PAD的面积是否存在最大值?若存在,请求出面积的最大值及此时点P的坐标;若不存在,请说明理由.
分析 (1)根据点的坐标满足函数解析式,可得C点坐标,根据待定系数法求函数解析式,可得答案;
(2)根据线段垂直平分线的性质,可得A点的对称点,根据两点之间线段最短,可得A′C与y轴的交点,根据自变量的值,可得相应的函数值;
(3)根据三角形的面积公式,可得关于n的二次函数,根据二次函数的性质,可得答案.
解答 解:(1)将点B 的坐标代入y2=$\frac{c}{x}$,得5=$\frac{c}{-1}$,解得c=-5.
∴反比例函数解析式为y2=-$\frac{5}{x}$,
将点C($\frac{5}{2}$,d)的坐标代入y2=-$\frac{5}{x}$,得d=-$\frac{5}{\frac{5}{2}}$=-2,
∴C($\frac{5}{2}$,-2),
∵一次函数y1=kx+b的图象经过B(-1,5)、C($\frac{5}{2}$,-2)两点,
∴$\left\{\begin{array}{l}{5=-k+b}\\{-2=\frac{5}{2}k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=3}\end{array}\right.$;
(2)如图: ;
;
一次函数的解析式为y=-2x+3,
当y=0时,-2x+3=0,解得x=$\frac{3}{2}$,即A($\frac{3}{2}$,0).
A点关于y轴的对称点是A′(-$\frac{3}{2}$,0),
A′C与y轴的交点是M点,
设A′C的函数解析式为y=kx+b,
将A′,C的坐标代入函数解析式,得
$\left\{\begin{array}{l}{\frac{5}{2}k+b=-2}\\{-\frac{3}{2}k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-\frac{3}{4}}\end{array}\right.$,
A′C的函数解析式为y=-$\frac{1}{2}$x-$\frac{3}{4}$,
当x=0时,y=-$\frac{3}{4}$,
即M(0,-$\frac{3}{4}$);
(3)存在,
令y1=0,即-2x+3=0,解得x=$\frac{3}{2}$,
∴A($\frac{3}{2}$,0),
由题意,点P(m,n)是一次函数y1=-2x+3的图象上的动点,且-1$<m<\frac{3}{2}$,
∴点P在线段AB上运动(不含A、B)
设P($\frac{3-n}{2}$,n)
∴DP∥x轴,且点D在y2=-$\frac{5}{x}$的图象上,
∴yD=yP=n,xD=-$\frac{5}{n}$,即D(-$\frac{5}{n}$,n).
∴△PAD的面积为S=$\frac{1}{2}$PD•OP=$\frac{1}{2}$•($\frac{3-n}{2}$+$\frac{5}{n}$)•n=-$\frac{1}{4}$(n-$\frac{3}{2}$)2+$\frac{49}{16}$.
∴S关于n的二次函数的图象开口向下,有最大值,
又∵n=-2m+3,-1<m<$\frac{3}{2}$,得0<n<5,而0<n=$\frac{3}{2}$<5,
∴当n=$\frac{3}{2}$时,即P($\frac{3}{4}$,$\frac{3}{2}$)时,△PAD的面积S最大,为$\frac{49}{16}$.
点评 本题考查了反比例函数综合题,(1)利用图象上的点满足函数解析式得出C点坐标,又利用待定系数法求函数解析式;(2)利用了线段垂直平分线的性质,线段的性质;(3)利用了三角形的面积公式得出函数解析式,又利用二次函数的性质:顶点坐标是函数的最值.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案| x | 0 | 0.5 | 1 | 1.1 | 1.2 | 1.3 |
| x2+px+q | -15 | -8.75 | -2 | -0.59 | 0.84 | 2.29 |
| A. | 0.5<x<1 | B. | 1<x<1.1 | C. | 1.1<x<1.2 | D. | 1.2<x<1.3 |
| A. | 有三个角相等 | B. | 有一条边和一个角相等 | ||
| C. | 有一条边和一个角相等 | D. | 有一条边和两个角相等 |
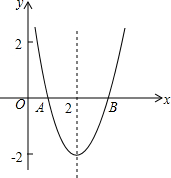 已知抛物线y=a(x-2)2+c如图所示,该抛物线与x轴交于A,B两点,点B的坐标为($\sqrt{7}$,0),试求方程a(x-2)2+c=0的两根.
已知抛物线y=a(x-2)2+c如图所示,该抛物线与x轴交于A,B两点,点B的坐标为($\sqrt{7}$,0),试求方程a(x-2)2+c=0的两根. 如图,AC⊥CB,AD为△ABC的中线,CG为高,DE⊥AD,BC=2AC,求证:AD=DF+DE.
如图,AC⊥CB,AD为△ABC的中线,CG为高,DE⊥AD,BC=2AC,求证:AD=DF+DE.