题目内容
11.已知抛物线y=-x2+(m-4)x+2m+4,与x轴交于A(x1,0),B(x2,0),与y轴交于C点,且x1,x2满足x1<x2,x1+2x2=0.(1)求抛物线的解析式;
(2)能否找到直线y=kx+b与抛物线交于P,Q两点,使y轴恰好平分△CPQ的面积,求出k,b所满足的条件.
分析 (1)根据一元二次方程的根与系数的关系,以及x1+2x2=0,求得m的值;
(2)y轴平分三角形CPQ面积,P,Q横坐标互为相反数,则把一次函数解析式代入二次函数解析式得到的一元二次方程的两个解的根的和是0,据此即可求解.
解答 解:(1)∵x1+x2=m-4,x1+2x2=0
∴x2=4-m
x1=2m-8
∵x1•x2=-(2m+4)=(4-m)(2m-8)
∴m=2或7,
∵x1<x2,即2m-8<4-m,
∴m<3,
∴m=2.
则抛物线的解析式是:y=-x2-2x+8;
(2)∵y轴平分三角形CPQ面积,
∴P,Q横坐标互为相反数
联立方程$\left\{\begin{array}{l}{y=-{x}^{2}-2x+8}\\{y=kx+b}\end{array}\right.$,
则x2+(2+k)x+b-8=0,
∵x1+x2=-(2+k)=0,
△=(2+k)2-4(b-8)>0,
解得:k=-2,b<8.
点评 本题考查了二次函数与一元二次方程,二次函数与x轴的交点的横坐标就是对应的方程的根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
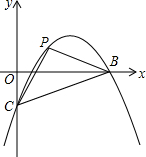 如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A,B,与y轴交于点C,点P为抛物线上一点,且△PBC的内外圆的圆心在x轴上,求点P的坐标.
如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A,B,与y轴交于点C,点P为抛物线上一点,且△PBC的内外圆的圆心在x轴上,求点P的坐标.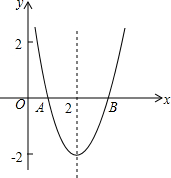 已知抛物线y=a(x-2)2+c如图所示,该抛物线与x轴交于A,B两点,点B的坐标为($\sqrt{7}$,0),试求方程a(x-2)2+c=0的两根.
已知抛物线y=a(x-2)2+c如图所示,该抛物线与x轴交于A,B两点,点B的坐标为($\sqrt{7}$,0),试求方程a(x-2)2+c=0的两根. 如图,AC⊥CB,AD为△ABC的中线,CG为高,DE⊥AD,BC=2AC,求证:AD=DF+DE.
如图,AC⊥CB,AD为△ABC的中线,CG为高,DE⊥AD,BC=2AC,求证:AD=DF+DE.