题目内容
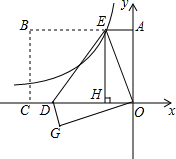 如图,在直角坐标系中,矩形OABC的顶点C在x轴的负半轴上,点A在y轴正半轴上,矩形OABC的面积为8
如图,在直角坐标系中,矩形OABC的顶点C在x轴的负半轴上,点A在y轴正半轴上,矩形OABC的面积为8| 2 |
| k |
| x |
考点:反比例函数综合题,反比例函数系数k的几何意义,全等三角形的判定与性质,矩形的判定与性质,轴对称的性质,相似三角形的判定与性质
专题:计算题
分析:连接BO与ED交于点Q,过点Q作QG⊥x轴,垂足为G,可通过三角形全等证得BO与ED的交点就是ED的中点F,由相似三角形的性质可得S△OGF=
S△OCB,根据反比例函数比例系数的几何意义可求出k,从而求出S△OAE,进而可以得到AB=4AE,即BE=3AE.由轴对称的性质可得OE=BE,从而得到OE=3AE,也就有AO=2
AE,根据△OAE的面积可以求出AE,OA的值.易证四边形OAEH为矩形,从而得到EH=OA,就可求出EH的值.
| 1 |
| 4 |
| 2 |
解答: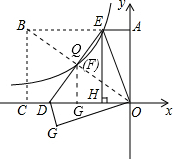 解:连接BO与ED交于点Q,过点Q作QG⊥x轴,垂足为G,如图所示,
解:连接BO与ED交于点Q,过点Q作QG⊥x轴,垂足为G,如图所示,
∵矩形OABC沿DE翻折,点B与点O重合,
∴BQ=OQ,BE=EO.
∵四边形OABC是矩形,
∴AB∥CO,∠BCO=∠OAB=90°.
∴∠EBQ=∠DOQ.
在△BEQ和△ODQ中,
.
∴△BEQ≌△ODQ(ASA).
∴EQ=DQ.
∴点Q是ED的中点.
∵∠QG0=∠BCO=90°,
∴QG∥BC.
∴△OGQ∽△OCB.
∴
=(
)2=(
)2=
.
∴S△OGQ=
S△OCB.
∵S矩形OABC=8
,
∴S△OCB=S△OAB=4
.
∴S△OGQ=
.
∵点F是ED的中点,
∴点F与点Q重合.
∴S△OGF=
.
∵点F在反比例函数y=
上,
∴
=
.
∵k<0,
∴k=-2
.
∴S△OAE=
=
.
∵S△OAB=4
,
∴AB=4AE.
∴BE=3AE.
由轴对称的性质可得:OE=BE.
∴OE=3AE.OA=
=2
AE.
∴S△OAE=
AO•AE=
×2
AE×AE=
.
∴AE=1.
∴OA=2
×1=2
.
∵∠EHO=∠HOA=∠OAE=90°,
∴四边形OAEH是矩形.
∴EH=OA=2
.
故答案分别为:-2
、2
.
 解:连接BO与ED交于点Q,过点Q作QG⊥x轴,垂足为G,如图所示,
解:连接BO与ED交于点Q,过点Q作QG⊥x轴,垂足为G,如图所示,∵矩形OABC沿DE翻折,点B与点O重合,
∴BQ=OQ,BE=EO.
∵四边形OABC是矩形,
∴AB∥CO,∠BCO=∠OAB=90°.
∴∠EBQ=∠DOQ.
在△BEQ和△ODQ中,
|
∴△BEQ≌△ODQ(ASA).
∴EQ=DQ.
∴点Q是ED的中点.
∵∠QG0=∠BCO=90°,
∴QG∥BC.
∴△OGQ∽△OCB.
∴
| S△OGQ |
| S△OCB |
| OQ |
| OB |
| OQ |
| 2OQ |
| 1 |
| 4 |
∴S△OGQ=
| 1 |
| 4 |
∵S矩形OABC=8
| 2 |
∴S△OCB=S△OAB=4
| 2 |
∴S△OGQ=
| 2 |
∵点F是ED的中点,
∴点F与点Q重合.
∴S△OGF=
| 2 |
∵点F在反比例函数y=
| k |
| x |
∴
| ||||
| 2 |
| 2 |
∵k<0,
∴k=-2
| 2 |
∴S△OAE=
| ||||
| 2 |
| 2 |
∵S△OAB=4
| 2 |
∴AB=4AE.
∴BE=3AE.
由轴对称的性质可得:OE=BE.
∴OE=3AE.OA=
| OE2-AE2 |
| 2 |
∴S△OAE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴AE=1.
∴OA=2
| 2 |
| 2 |
∵∠EHO=∠HOA=∠OAE=90°,
∴四边形OAEH是矩形.
∴EH=OA=2
| 2 |
故答案分别为:-2
| 2 |
| 2 |
点评:本题考查了反比例函数比例系数的几何意义、轴对称的性质、全等三角形的判定与性质、矩形的判定与性质、相似三角形的判定与性质等知识,有一定的综合性.

练习册系列答案
相关题目
一个直角三角形的两条直角边分别为5、12,则第三边长为( )
| A、13 | ||
B、13或
| ||
C、
| ||
| D、7 |
 如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB:AD=2:3,那么tan∠EFC值是
如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB:AD=2:3,那么tan∠EFC值是