题目内容
 如图,点O是△ABC的两条角平分线的交点,若∠A=80°,则∠BOC的大小是
如图,点O是△ABC的两条角平分线的交点,若∠A=80°,则∠BOC的大小是考点:三角形内角和定理
专题:
分析:先根据三角形内角和定理得出∠ABC+∠ACB的度数,再由角平分线的定义得出∠1=∠2,∠3=∠4,再根据三角形内角和定理求出∠2+∠4的度数,进而可得出∠BOC的度
解答: 解:∵△ABC中,∠A=80°,
解:∵△ABC中,∠A=80°,
∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,
∵OB、OC分别是∠ABC、∠ACB的平分线,
∴∠1=∠2=
∠ABC,∠3=∠4=
∠ACB,
∴∠2+∠4=
(∠ABC+∠ACB)=
×100°=50°,
∴∠BOC=180°-(∠2+∠4)=180°-50°=130°.
故答案为:130°.
 解:∵△ABC中,∠A=80°,
解:∵△ABC中,∠A=80°,∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,
∵OB、OC分别是∠ABC、∠ACB的平分线,
∴∠1=∠2=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠2+∠4=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠2+∠4)=180°-50°=130°.
故答案为:130°.
点评:本题考查的是三角形内角和定理及角平分线的性质,熟知三角形的内角和为180°是解答此题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气道步行1000米到达点C处,测得M小区位于点C的北偏西75°方向,试在主输气管道AC上寻找支管道连接点N,使其到该小区铺设的管道最短,此时AN的长约是(参考:
如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气道步行1000米到达点C处,测得M小区位于点C的北偏西75°方向,试在主输气管道AC上寻找支管道连接点N,使其到该小区铺设的管道最短,此时AN的长约是(参考:| 2 |
| 3 |
| A、366 | B、634 |
| C、650 | D、700 |
某水坝的坡度i=1:
,水平长度AB=10
米,则坝的高度为( )
| 3 |
| 3 |
| A、10米 | ||
| B、20米 | ||
| C、40米 | ||
D、10
|
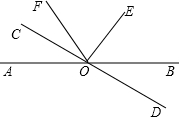 如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=28°,求∠BOD的度数.
如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=28°,求∠BOD的度数. 在等腰直角△ABC中,∠C=90°,AC=6,D为AC上一点,若tan∠DBC=
在等腰直角△ABC中,∠C=90°,AC=6,D为AC上一点,若tan∠DBC= 请观察如图的立体图形,分别画出从正面、左面、上面看到的平面图形.
请观察如图的立体图形,分别画出从正面、左面、上面看到的平面图形.