题目内容
19.一辆汽车开往距离出发地180km的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40min到达目的地,求前一小时的行驶速度.设原计划行驶的速度为xkm/h.(1)根据题意填写下表(要求:填上适当的代数式,完成表格)
| 速度(km/h) | 所走的路程(km) | 所用时间(h) | |
| 出发后第一小时内行驶 | x | x | 1 |
| 出发一小时以后行驶 | 1.5x | 180-x | $\frac{180-x}{1.5x}$ |
| 原计划行驶 | x | 180 | $\frac{180}{x}$ |
分析 (1)根据题意和表格中的数据可以把表格补充完整;
(2)根据题意可以列出相应的分式方程,从而可以解答本题.
解答 解:(1)由题意可得,
出发一小时以后行驶是速度为1.5x,所用的时间为:$\frac{180-x}{1.5x}$,
原计划行驶的时间为:$\frac{180}{x}$,
故答案为:1.5x,$\frac{180-x}{1.5x}$,$\frac{180}{x}$;
(2)由题意可得,
$\frac{180-x}{1.5x}+1+\frac{40}{60}=\frac{180}{x}$,
解得,x=60
经检验x=60时,1.5x≠0,
∴x=60是原分式方程的解,
即原计划行驶的速度为60km/h.
点评 本题考查分式方程的应用,解题的关键是明确题意,找出所求问题需要的条件,注意要验根.

练习册系列答案
相关题目
9.五棱柱的顶点总个数有( )个.
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
4.某检修小组从A地出发,在东西方向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下(单位:km):
(1)求收工时检修小组距A地多远;
(2)在第五次记录时时检修小组距A地最远;
(3)若每千米耗油0.1L,每升汽油需6.0元,问检修小组工作一天需汽油费多少元?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -3 | +8 | -9 | +10 | +4 | -6 | -2 |
(2)在第五次记录时时检修小组距A地最远;
(3)若每千米耗油0.1L,每升汽油需6.0元,问检修小组工作一天需汽油费多少元?
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=12$\sqrt{2}$cm,动点P从点A出发,沿AB方向以每秒2cm的速度向终点B运动,同时,动点Q从点B出发沿BC方向以每秒$\sqrt{2}$cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为P′,设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为4.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=12$\sqrt{2}$cm,动点P从点A出发,沿AB方向以每秒2cm的速度向终点B运动,同时,动点Q从点B出发沿BC方向以每秒$\sqrt{2}$cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为P′,设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为4.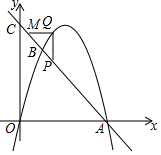 如图,在平面直角坐标系中,点A是抛物线y=-$\frac{1}{2}$x2+4x与x轴正半轴的交点,点B在抛物线上,其横坐标为2,直线AB与y轴交于点C.点M、P在线段AC上(不含端点),点Q在抛物线上,且MQ平行于x轴,PQ平行于y轴.设点P横坐标为m.
如图,在平面直角坐标系中,点A是抛物线y=-$\frac{1}{2}$x2+4x与x轴正半轴的交点,点B在抛物线上,其横坐标为2,直线AB与y轴交于点C.点M、P在线段AC上(不含端点),点Q在抛物线上,且MQ平行于x轴,PQ平行于y轴.设点P横坐标为m. 在矩形ABCD中,AB=6,BC=8,△ABD绕B点顺时针旋转90°到△BEF,连接DF,则DF=10$\sqrt{2}$.
在矩形ABCD中,AB=6,BC=8,△ABD绕B点顺时针旋转90°到△BEF,连接DF,则DF=10$\sqrt{2}$.