题目内容
7. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=12$\sqrt{2}$cm,动点P从点A出发,沿AB方向以每秒2cm的速度向终点B运动,同时,动点Q从点B出发沿BC方向以每秒$\sqrt{2}$cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为P′,设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为4.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=12$\sqrt{2}$cm,动点P从点A出发,沿AB方向以每秒2cm的速度向终点B运动,同时,动点Q从点B出发沿BC方向以每秒$\sqrt{2}$cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为P′,设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为4.
分析 连接PP′交CQ于D,根据菱形的对角线互相垂直平分可得PP′⊥CQ,CD=DQ,用t表示出CD,过点P作PO⊥AC于O,可得四边形CDPO是矩形,再判断出△ABC是等腰直角三角形,根据等腰直角三角形的性质可得∠A=45°,从而得到△APO是等腰直角三角形,再用t表示出PO,然后根据矩形的对边相等列出方程求解即可.
解答 解: 解:如图,连接PP′交CQ于D,
解:如图,连接PP′交CQ于D,
∵四边形QPCP′为菱形,
∴PP′⊥CQ,CD=DQ,
∵点Q的速度是每秒1cm,
∴CD=$\frac{1}{2}$CQ=$\frac{1}{2}$(12$\sqrt{2}$-$\sqrt{2}$t)cm,
过点P作PO⊥AC于O,
则四边形CDPO是矩形,
∴CD=PO,
∵∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴∠A=45°,
∴PO=$\frac{\sqrt{2}}{2}$AP,
∵点P的运动速度是每秒 2cm,
∴PO=$\frac{\sqrt{2}}{2}$×2t=$\sqrt{2}$tcm,
∴$\frac{1}{2}$(12$\sqrt{2}$-$\sqrt{2}$t)=$\sqrt{2}$t,
解得t=4,
故答案为4
点评 本题考查了翻折变换,菱形的判定与性质,等腰直角三角形的性质,作辅助线构造出矩形和等腰直角三角形是解题的关键.

练习册系列答案
相关题目
18.下列图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.一辆汽车开往距离出发地180km的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40min到达目的地,求前一小时的行驶速度.设原计划行驶的速度为xkm/h.
(1)根据题意填写下表(要求:填上适当的代数式,完成表格)
(2)列出方程(组),并求出问题的解.
(1)根据题意填写下表(要求:填上适当的代数式,完成表格)
| 速度(km/h) | 所走的路程(km) | 所用时间(h) | |
| 出发后第一小时内行驶 | x | x | 1 |
| 出发一小时以后行驶 | 1.5x | 180-x | $\frac{180-x}{1.5x}$ |
| 原计划行驶 | x | 180 | $\frac{180}{x}$ |
16.下列从左到右的变形是因式分解的是( )
| A. | 6a2b2=3ab•2ab | B. | -8x2+8x-2=-2(2x-1)2 | ||
| C. | 2x2+8x-1=2x(x+4)-1 | D. | a2-1=a(a-$\frac{1}{a}$) |

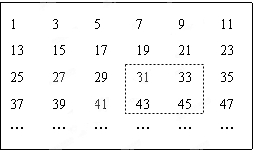 将连续的奇数1,3,5,7,9…排成如图所示的数表,用长方形框选其中的四个数.
将连续的奇数1,3,5,7,9…排成如图所示的数表,用长方形框选其中的四个数.