题目内容
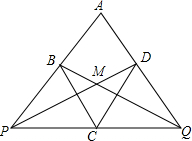 如图,菱形ABCD中,∠A=60°,过顶点C任意作一直线分别交AB、AD的延长线于P、Q两点,设PD、QB相交于点M.求证:∠PMQ=120°.
如图,菱形ABCD中,∠A=60°,过顶点C任意作一直线分别交AB、AD的延长线于P、Q两点,设PD、QB相交于点M.求证:∠PMQ=120°.考点:菱形的性质,相似三角形的判定与性质
专题:证明题
分析:连接BD,利用等边三角形的判定与性质得出△ABD为等边三角形,进而得出△PBC∽△CDQ,再利用已知得出△PBD∽△BDQ,求出△BMD∽△BDQ进而得出答案.
解答: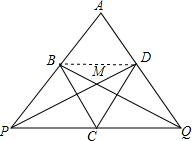 证明:连接BD,
证明:连接BD,
∵四边形ABCD是菱形,
∴BC=CD=AB=AD,
∵∠A=60°,
∴△ABD为等边三角形,
∵BC∥AD,AB∥CD,
∴∠BPC=∠DCQ,∠BCP=∠DQC,
∴△PBC∽△CDQ,
∴
=
,
∵BC=CD=BD,
∴BD2=PB×DQ,
∴
=
,
∵∠PBD=∠BDQ=120°,
∴△PBD∽△BDQ,
∴∠BDM=∠DQB,
∵∠BDM=∠DBQ,
∴△BMD∽△BDQ,
∴∠BMD=∠BDQ=120°.
 证明:连接BD,
证明:连接BD,∵四边形ABCD是菱形,
∴BC=CD=AB=AD,
∵∠A=60°,
∴△ABD为等边三角形,
∵BC∥AD,AB∥CD,
∴∠BPC=∠DCQ,∠BCP=∠DQC,
∴△PBC∽△CDQ,
∴
| PB |
| BC |
| DC |
| DQ |
∵BC=CD=BD,
∴BD2=PB×DQ,
∴
| BD |
| PB |
| DQ |
| BD |
∵∠PBD=∠BDQ=120°,
∴△PBD∽△BDQ,
∴∠BDM=∠DQB,
∵∠BDM=∠DBQ,
∴△BMD∽△BDQ,
∴∠BMD=∠BDQ=120°.
点评:此题主要考查了菱形的性质以及等边三角形的判定与性质和相似三角形的判定与性质等知识,得出△PBC∽△CDQ是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
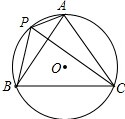 如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°.
如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°.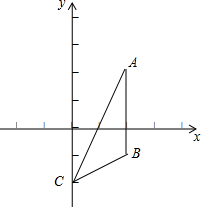 如图,点A、B、C的坐标分别是(2,2),(2,-1),(0,-2).
如图,点A、B、C的坐标分别是(2,2),(2,-1),(0,-2).