题目内容
6.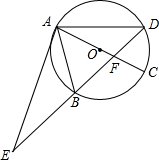 如图,⊙O的直径AC与弦BD交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
如图,⊙O的直径AC与弦BD交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,已知⊙O的半径为3,CF:AF=1:2.求AE的长.
分析 (1)连接CD,由圆周角定理得出∠ADC=90°,∠BAC=∠EDC,得出∠ADB+∠EDC=90°,证出∠EAC=90°,即可得出结论;
(2)连接BC,由圆周角定理得出∠ABC=90°,∠CBA=∠ABC=90°,由直角三角形斜边上的中线性质得出AB=$\frac{1}{2}$EF=BF,得出∠BAC=∠AFE,证明△EAF∽△CBA,得出$\frac{AF}{AB}=\frac{EF}{AC}$,求出AB,再根据勾股定理求出AE即可.
解答 (1)证明:如图1所示: 连接CD,
连接CD,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠ADB+∠EDC=90°,
∵∠BAC=∠EDC,∠EAB=∠ADB,
∴∠EAC=∠EAB+∠BAC=90°,即EA⊥OA,
∴EA是⊙O的切线;
(2)解:如图2所示: 连接BC,
连接BC,
∵AC是⊙O的直径,
∴∠ABC=90°,
∴∠CBA=∠ABC=90°
∵∠EAF=90°,B是EF的中点,
∴AB=$\frac{1}{2}$EF=BF,
∴∠BAC=∠AFE,
∴△EAF∽△CBA,
∴$\frac{AF}{AB}=\frac{EF}{AC}$,
∵⊙O的半径为3,CF:AF=1:2,
∴AC=6,AF=4,CF=2,
∴$\frac{4}{AB}=\frac{2AB}{6}$,
解得:AB=2$\sqrt{3}$,
∴EF=4$\sqrt{3}$,
∴AE=$\sqrt{E{F}^{2}-A{F}^{2}}$=$\sqrt{(4\sqrt{3})^{2}-{4}^{2}}$=4$\sqrt{2}$.
点评 本题考查了切线的判定、勾股定理、相似三角形的判定与性质、直角三角形斜边上的中线性质、圆周角定理;本题有一定难度,特别是(2)中,需要证明三角形相似和勾股定理才能得出结果.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 到公园里调查100名晨练老人 | |
| B. | 到医院调查100名老年病人 | |
| C. | 到某小区调查10名老年居民 | |
| D. | 利用户籍资料,按规则抽查10%的老年人 |
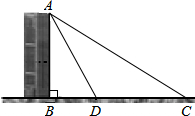 如图,为了测量楼AB的高度,小明在点C处测得楼AB的顶端A的仰角为30°,又向前走了20米后到达点D,点B、D、C在同一条直线上,并在点D测得楼AB的顶端A的仰角为60°,求楼AB的高.
如图,为了测量楼AB的高度,小明在点C处测得楼AB的顶端A的仰角为30°,又向前走了20米后到达点D,点B、D、C在同一条直线上,并在点D测得楼AB的顶端A的仰角为60°,求楼AB的高.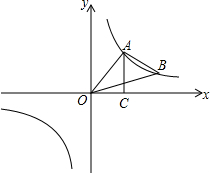 如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0)的图象上,且点A,B的横坐标分别为a和2a(a>0).过点A作x轴的垂线,垂足为C,连接OA,△AOC的面积为2.
如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0)的图象上,且点A,B的横坐标分别为a和2a(a>0).过点A作x轴的垂线,垂足为C,连接OA,△AOC的面积为2.