题目内容
14.抛物线y=(x-1)(x-3)与x轴交于A、B两点,顶点为C,则△ABC的外接圆的圆心坐标为(2,0).分析 求出点A、B、C的坐标,根据勾股定理逆定理知△ABC为等腰直角三角形,故△ABC的外接圆的圆心为AB的中点,即可求出圆心坐标.
解答 解:令y=0,0=(x-1)(x-3)
解得:x1=1,x2=3,
∴A(1,0)、B(3,0),
∵y=(x-1)(x-3)=(x-2)2-1,
∴顶点C(2,-1)
∵AB=2,AC=BC=$\sqrt{2}$,
∴△ABC为等腰直角三角形,
∴△ABC的外接圆的圆心为AB的中点,
∴外接圆的圆心坐标为(2,0).
故答案为:(2,0).
点评 本题考查了抛物线与坐标轴的交点坐标、勾股定理的逆定理以及三角形外接圆的性质,求出A、B、C的坐标是解决问题的关键.

练习册系列答案
相关题目
5.如图,把一张长为10,宽为8的矩形硬纸板四周各剪去一个边长为a的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计),折成的长方体盒子的底面周长为( )


| A. | 18-2a | B. | 18-4a | C. | 36-4a | D. | 36-8a |

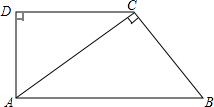 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,