题目内容
4.已知关于x的方程mx2-(m+2)x+2=0(m≠0).(1)求证:方程总有两个实数根;
(2)已知方程有两个不相等的实数根α,β,满足$\frac{1}{α}$+$\frac{1}{β}$=1,求m的值.
分析 (1)m≠0时是一元二次方程,求得方程根的判别式,证明其总大于或等于0即可;
(2)利用根与系数的关系分别求得αβ和α+β,代入可得到关于m的方程,求其即可.
解答 (1)证明:∵方程mx2-(m+2)x+2=0(m≠0)是一元二次方程,
∴△=(m+2)2-8m=m2+4m+4-8m=m2-4m+4=(m-2)2≥0,
∴方程总有两个实数根;
(2)解:∵方程有两个不相等的实数根α,β,
∴由根与系数的关系可得α+β=$\frac{m+2}{m}$,αβ=$\frac{2}{m}$,
∵$\frac{1}{α}$+$\frac{1}{β}$=1,
∴$\frac{\frac{m+2}{m}}{\frac{2}{m}}$=$\frac{m+2}{2}$=1,
解得m=0,
∵m≠0,
∴m无解.
点评 本题主要考查一元二次方程根的判别及根与系数的关系,掌握一元二次方程根的判别式与根的情况是解题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
13.下列语句正确的是( )
| A. | $\frac{125}{216}$的立方根是±$\frac{5}{6}$ | B. | -3是27的负的立方根 | ||
| C. | $\sqrt{64}$的立方根是2 | D. | (-1)2的立方根是-1 |
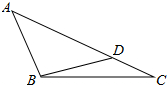 已知:如图,在△ABC中,AC=9,BC=6,请问,在边AC上是否存在一点D,使△ABC∽△BDC?若存在请求出CD的长,若不存在,请说明理由.
已知:如图,在△ABC中,AC=9,BC=6,请问,在边AC上是否存在一点D,使△ABC∽△BDC?若存在请求出CD的长,若不存在,请说明理由.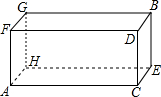 有一长方体纸盒,如图所示小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长AC为12.宽CE为9.高CD为7,请你帮助该小组计算出由A到B的最短路线.
有一长方体纸盒,如图所示小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长AC为12.宽CE为9.高CD为7,请你帮助该小组计算出由A到B的最短路线.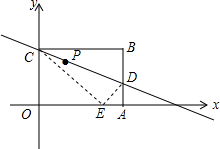 如图,在平面直角坐标系中,矩形OABC的顶点A(10,0),C(0,8),现将矩形OABC沿直线CD折叠,使点B落在x轴上的E处.
如图,在平面直角坐标系中,矩形OABC的顶点A(10,0),C(0,8),现将矩形OABC沿直线CD折叠,使点B落在x轴上的E处.