题目内容
16．若要使分式$\frac{2x+2}{{{{（{x+1}）}^2}}}$的值为整数，则整数x可取的个数为（ ）| A． | 5个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 原式约分化简后，根据值为整数确定出整数x的取值个数即可．
解答 解：原式=$\frac{2（x+1）}{（x+1）^{2}}$=$\frac{2}{x+1}$，
由结果为整数，得到x+1=±1或±2，整数x为0，-2，1，-3共4个，
故选4
点评 此题考查了分式的值，认真审题，抓住关键的字眼，是正确解题的出路．如本题“整数x”中的“整数”，“$\frac{2}{x+1}$的值为整数”中的“整数”．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
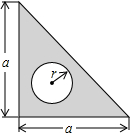一块三角尺的形状和尺寸如图所示，如果空孔的半径是r，三角尺的厚度是h，用式子表示这块三角尺的体积V．若a=6cm，r=0.5cm，h=0.2cm，求V的值（π取3）
要给一个长、宽、高分别为x，y，z的箱子打包，其打包方式如图所示．
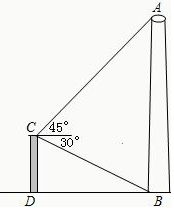如图，在城市改造时，要拆除建筑物AB，在离它21米远的建筑物CD顶端C测得A的仰角45°，B的俯角30°，在点B的35米处有一文物，问：此文物是否在危险区内？请说明理由．（参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）
如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E．