题目内容
8.已知等腰△ABC内接于⊙O,且顶角∠A=70°,求$\widehat{AB}$,$\widehat{BC}$,$\widehat{AC}$的度数.
分析 根据弧的度数就是这段弧所对的圆心角的度数,由题意可以分别求得∠B和∠C的度数,从而可以得到$\widehat{AB}$,$\widehat{BC}$,$\widehat{AC}$的度数.
解答 解:∵等腰△ABC内接于⊙O,且顶角∠A=70°,
∴∠B=∠C=(180°-70°)÷2=55°,
∴∠BOC=140°,∠AOB=110°,∠AOC=110°,
即$\widehat{AB}$的度数是110°,$\widehat{BC}$的度数是140°,$\widehat{AC}$的度数是110°.
点评 本题考查三角形的外接圆、弧的度数、圆周角与圆心角的关系,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
18.已知x=-1是一元二次方程x2+mx+n=0的一个根,则(m-n)2的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
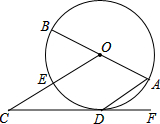 如图,AB是⊙O的直径,点D是⊙O上的一点,OC∥AD交⊙O于点E,点F在CD的延长线上,∠BOC+∠ADF=90°.
如图,AB是⊙O的直径,点D是⊙O上的一点,OC∥AD交⊙O于点E,点F在CD的延长线上,∠BOC+∠ADF=90°. 如图,已知直线a∥b,直线c与a、b分别交于A、B,且∠1=120°,则∠2=120°.
如图,已知直线a∥b,直线c与a、b分别交于A、B,且∠1=120°,则∠2=120°.