题目内容
 如图,正方形ABCD中,AC为对角线,E、F分别是边AB、AD上的两点,且CE=CF.求证:AE=AF.
如图,正方形ABCD中,AC为对角线,E、F分别是边AB、AD上的两点,且CE=CF.求证:AE=AF.考点:正方形的性质,全等三角形的判定与性质
专题:证明题
分析:先证出△EBC≌△EFC,再证出△AFC≌△AEC,即可证出AE=AF.
解答:证明:在Rt△EBC和Rt△FDC中,
,
∴Rt△EBC≌Rt△EFC(HL),
∴∠BEC=∠DFC,
∴∠AEC=180°-∠BEC,
∠AFC=180°-∠DFC,
∴∠AEC=∠AFC,
在△AFC和△AEC中,
∴△AFC≌△AEC(AAS),
∴AE=AF.
|
∴Rt△EBC≌Rt△EFC(HL),
∴∠BEC=∠DFC,
∴∠AEC=180°-∠BEC,
∠AFC=180°-∠DFC,
∴∠AEC=∠AFC,
在△AFC和△AEC中,
|
∴△AFC≌△AEC(AAS),
∴AE=AF.
点评:此题考查了正方形的性质,三角形全等的判定与性质,掌握三角形全等的判定方法是解决问题的关键.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图,AE∥BC,∠B=∠C=50°,求∠DAC的度数.
如图,AE∥BC,∠B=∠C=50°,求∠DAC的度数.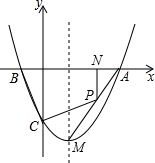 已知抛物线的图象经过点A(3,0)、点B(-1,0)、点C(0,-3),点M是抛物线上的顶点,点P是线段AM上一动点(不与点A、M重合),PN垂直x轴于点N.
已知抛物线的图象经过点A(3,0)、点B(-1,0)、点C(0,-3),点M是抛物线上的顶点,点P是线段AM上一动点(不与点A、M重合),PN垂直x轴于点N.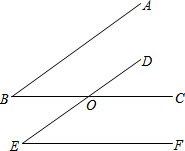 已知如图BC交DE于O,给出下面三个论断:
已知如图BC交DE于O,给出下面三个论断: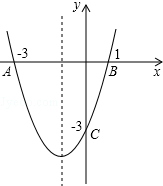 如图,抛物线l交x轴于点A(-3,0)、B(1,0),交y轴于点C(0,-3).将抛物线l沿y轴翻折得抛物线l1.
如图,抛物线l交x轴于点A(-3,0)、B(1,0),交y轴于点C(0,-3).将抛物线l沿y轴翻折得抛物线l1. 已知:如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.如果AC=2,CE=4.
已知:如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.如果AC=2,CE=4.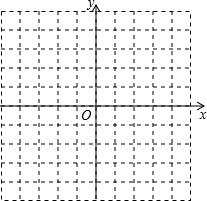 如图,已知在平面直角坐标系中,点A(1,-1),B(-1,4),C(-3,1).
如图,已知在平面直角坐标系中,点A(1,-1),B(-1,4),C(-3,1).