题目内容
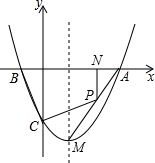 已知抛物线的图象经过点A(3,0)、点B(-1,0)、点C(0,-3),点M是抛物线上的顶点,点P是线段AM上一动点(不与点A、M重合),PN垂直x轴于点N.
已知抛物线的图象经过点A(3,0)、点B(-1,0)、点C(0,-3),点M是抛物线上的顶点,点P是线段AM上一动点(不与点A、M重合),PN垂直x轴于点N.(1)求抛物线的解析式及点M的坐标;
(2)求直线AM的解析式;
(3)若设点P的横坐标为x,四边形BCPN的面积为S,写出S与x之间的函数关系式,并写出自变量x的取值范围;
(4)当x为何值时,S有最大值,最大值是多少?
考点:二次函数综合题
专题:
分析:(1)直接利用待定系数法求二次函数解析式,进而利用配方法求出其顶点坐标即可;
(2)利用(1)中所求,再利用待定系数法求一次函数解析式即可;
(3)分别表示出S△BOC=
×1×3=
,S四边形OCPN=
(6-2x+3)×x=-x2+
x,进而得出S与x的函数关系,利用M,A点坐标得出x的取值范围;
(4)利用配方法求出二次函数最值即可.
(2)利用(1)中所求,再利用待定系数法求一次函数解析式即可;
(3)分别表示出S△BOC=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
(4)利用配方法求出二次函数最值即可.
解答:解:(1)设抛物线解析式为:y=ax2+bx+c,将点A(3,0)、点B(-1,0)、点C(0,-3)代入得出:
,
解得:
.
故抛物线解析式为:y=x2-2x-3;
y=x2-2x-3=(x-1)2-4,
则M点坐标为:(1,-4).
(2)设直线AM的解析式为:y=kx+d,
将A,M点代入得出:
,
解得:
.
故直线AM的解析式为:y=2x-6;
(3)设点P的横坐标为x,四边形BCPN的面积为S,
∵PN垂直x轴于点N,
∴NO=x,PN=-y=6-2x,
∴S△BOC=
×1×3=
,
S四边形OCPN=
(6-2x+3)×x=-x2+
x
故S与x之间的函数关系式为:S=S△BOC+S四边形OCPN=-x2+
x+
,
自变量x的取值范围是:1<x<3;
(4)由(2)得:S=-x2+
x+
=-(x2-
x)+
=-(x-
)2+
,
故当x=
时,S有最大值,最大值是
.
|
解得:
|
故抛物线解析式为:y=x2-2x-3;
y=x2-2x-3=(x-1)2-4,
则M点坐标为:(1,-4).
(2)设直线AM的解析式为:y=kx+d,
将A,M点代入得出:
|
解得:
|
故直线AM的解析式为:y=2x-6;

(3)设点P的横坐标为x,四边形BCPN的面积为S,
∵PN垂直x轴于点N,
∴NO=x,PN=-y=6-2x,
∴S△BOC=
| 1 |
| 2 |
| 3 |
| 2 |
S四边形OCPN=
| 1 |
| 2 |
| 9 |
| 2 |
故S与x之间的函数关系式为:S=S△BOC+S四边形OCPN=-x2+
| 9 |
| 2 |
| 3 |
| 2 |
自变量x的取值范围是:1<x<3;
(4)由(2)得:S=-x2+
| 9 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
| 105 |
| 16 |
故当x=
| 9 |
| 4 |
| 105 |
| 16 |
点评:此题主要考查了二次函数综合以及待定系数法求二次函数解析式以及求一次函数解析式和四边形面积求法和二次函数最值求法,注意表示出PN的长是解题关键.

练习册系列答案
相关题目
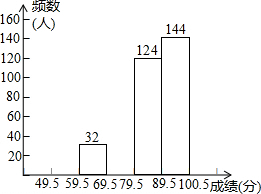 某市七年级有10000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分进行统计请你根据不完整的频率分布表.解答下列问题:
某市七年级有10000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分进行统计请你根据不完整的频率分布表.解答下列问题: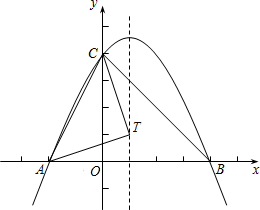 如图,抛物线y=ax2+bx+4(a≠0)与x轴交于点A(-2,0)和B(4,0)、与y轴交于点C.
如图,抛物线y=ax2+bx+4(a≠0)与x轴交于点A(-2,0)和B(4,0)、与y轴交于点C. 已知:a、b、c为正实数,抛物线y=x2-2ax+b2与x轴交于M、N两点,交y轴于P点其中M的坐标(a+c,0).
已知:a、b、c为正实数,抛物线y=x2-2ax+b2与x轴交于M、N两点,交y轴于P点其中M的坐标(a+c,0).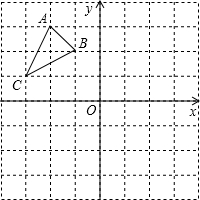 如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(-2,3)、B(-1,2)、C(-3,1),△ABC绕点O顺时针旋转90°后得到△A1B1C1.
如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(-2,3)、B(-1,2)、C(-3,1),△ABC绕点O顺时针旋转90°后得到△A1B1C1. 如图,正方形ABCD中,AC为对角线,E、F分别是边AB、AD上的两点,且CE=CF.求证:AE=AF.
如图,正方形ABCD中,AC为对角线,E、F分别是边AB、AD上的两点,且CE=CF.求证:AE=AF.