题目内容
19.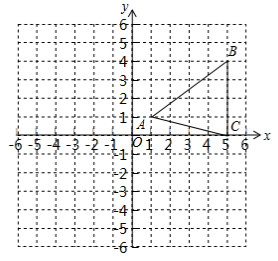 如图,在平面直角坐标系中,△ABC的顶点为A(1,1),B(5,4),C(5,0).
如图,在平面直角坐标系中,△ABC的顶点为A(1,1),B(5,4),C(5,0).(1)作出△ABC关于y轴的对称图形△A1B1C1;
(2)请直接写出下列各点的坐标:A1 (-1,1),B1 (-5,4);
(3)填空:△A1B1C1的周长为9+$\sqrt{17}$.
分析 (1)作出各点关于y轴的对称点,再顺次连接即可;
(2)根据各点在坐标系中的位置写出各点坐标即可;
(3)利用勾股定理求出三角形的各边长,再求出其周长即可.
解答  解:(1)如图,△A1B1C1即为所求;
解:(1)如图,△A1B1C1即为所求;
(2)由图可知,A1(-1,1),B1(-5,4).
故答案为:(-1,1),(-5,4);
(3)∵A1B1=$\sqrt{(5-1)^{2}+(4-1)^{2}}$=5,B1C1=4,A1C1=$\sqrt{(5-1)^{2}+(0-1)^{2}}$=$\sqrt{17}$,
A1B1C1的周长=5+4+$\sqrt{17}$=9+$\sqrt{17}$.
故答案为:9+$\sqrt{17}$.
点评 本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
10.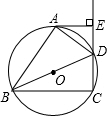 如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
 如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.(1)求证:AE是⊙O的切线;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
4.下列运算正确的是( )
| A. | a3+a3=a6 | B. | (a2)3=a5 | C. | a2•a3=a5 | D. | a6÷a3=a2 |
 如图,菱形ABCD中,对角线AC=10,BD=24,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是13.
如图,菱形ABCD中,对角线AC=10,BD=24,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是13. 如图,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到点B为止,点Q以2cm/s的速度向点D移动(P点停止移动时,点Q也停止移动).设移动时间为t(s),问
如图,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到点B为止,点Q以2cm/s的速度向点D移动(P点停止移动时,点Q也停止移动).设移动时间为t(s),问