题目内容
9. 如图,菱形ABCD中,对角线AC=10,BD=24,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是13.
如图,菱形ABCD中,对角线AC=10,BD=24,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是13.
分析 要求PM+PN的最小值,PM、PN不能直接求,可考虑通过作辅助线转化PN、PM的值,从而找出其最小值求解.
解答 解:如图:
作ME⊥AC交AD于E,连接EN,
则EN就是PM+PN的最小值,
∵M、N分别是AB、BC的中点,
∴BN=BM=AM,
∵ME⊥AC交AD于E,
∴AE=AM,
∴AE=BN,AE∥BN,
∴四边形ABNE是平行四边形,
∴EN=AB,EN∥AB,
而由题意可知,可得AB=$\sqrt{(10÷2)^{2}+(24÷2)^{2}}=13$,
∴EN=AB=13,
∴PM+PN的最小值为13.
故答案为:13
点评 此题考查菱形的性质和轴对称及平行四边形的判定等知识的综合应用.综合运用这些知识是解决本题的关键.

练习册系列答案
相关题目
19.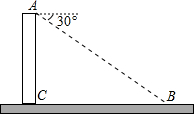 如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为( )
如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为( )
 如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为( )
如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为( )| A. | 15m | B. | 20m | C. | 10$\sqrt{3}$m | D. | 20$\sqrt{3}$m |
20.下列图形中,是中心对称图形又是轴对称图形的有( )
①平行四边形;②菱形;③矩形;④正方形;⑤等腰梯形;⑥线段;⑦角.
①平行四边形;②菱形;③矩形;④正方形;⑤等腰梯形;⑥线段;⑦角.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
14.已知a>0,b<0,且a的绝对值小于b的绝对值,则直线y=ax+b和直线y=bx+a相交于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.式子22×(22)4的计算结果用幂的形式表示正确的是( )
| A. | 27 | B. | 28 | C. | 210 | D. | 212 |
 小明家门前有一块空地,空地外有一面长10米的围墙,为了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买回了32米长的不锈钢管准备作为花圃的围栏(如图所示),花圃的一边AD(垂直围墙的边)究竟应为多少米才能使花圃的面积最大?
小明家门前有一块空地,空地外有一面长10米的围墙,为了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买回了32米长的不锈钢管准备作为花圃的围栏(如图所示),花圃的一边AD(垂直围墙的边)究竟应为多少米才能使花圃的面积最大?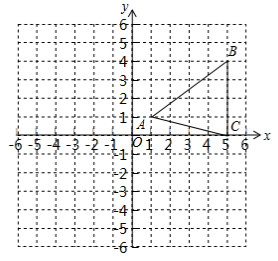 如图,在平面直角坐标系中,△ABC的顶点为A(1,1),B(5,4),C(5,0).
如图,在平面直角坐标系中,△ABC的顶点为A(1,1),B(5,4),C(5,0).