题目内容
9. 如图,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到点B为止,点Q以2cm/s的速度向点D移动(P点停止移动时,点Q也停止移动).设移动时间为t(s),问
如图,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到点B为止,点Q以2cm/s的速度向点D移动(P点停止移动时,点Q也停止移动).设移动时间为t(s),问(1)四边形APDQ的形状可能为矩形吗?如果能,求出t的值;若不能,请说明理由;
(2)当t为何值时,P、Q两点间距离是10cm?
(3)分别连接DP、CP,△DPC可能为直角三角形吗?若能,求出t的值;若不能,请说明理由.
分析 (1)利用矩形的性质得出当AP=DQ时,四边形APQD为矩形求出即可;
(2)设当t秒时PQ=10cm,利用勾股定理得出即可;
(3)要使△PCD为直角三角形,必有点P到线段中点距离等于CD的一半即可解决问题.
解答 解:(1)四边形APDQ的形状有可能为矩形;
理由:如图,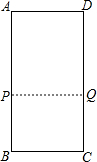
当四边形APQD为矩形,则AP=DQ,
即3t=16-2t,
解得:t=$\frac{16}{5}$.
答:当$\frac{16}{5}$秒时四边形APQD为矩形;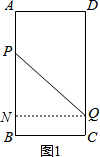 解:(2)如图1,过点Q作ON⊥AB于点N,
解:(2)如图1,过点Q作ON⊥AB于点N,
设当t秒时PQ=10cm,
则QC=2t,PN=16-5t,
故62+(16-5t)2=100,
解得:t1=$\frac{8}{5}$,t2=$\frac{24}{5}$,
答:$\frac{8}{5}$秒或$\frac{24}{5}$秒时点P和点Q之间的距离是10cm;
(3)△DPC有可能为直角三角形,
理由:如图2,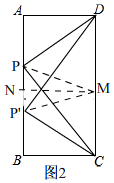 过矩形的边CD中点M作MN⊥AB,连接PM,
过矩形的边CD中点M作MN⊥AB,连接PM,
∴MN=AD=6,AN=$\frac{1}{2}$AB=8,
要使△DPC为直角三角形,
∴PM=$\frac{1}{2}$CD=$\frac{1}{2}$AB=8,
在Rt△PMN中,PN2=PM2-MN2,
∴PN2=64-36=28,
∴PN=2$\sqrt{7}$,
由运动知,AP=3t,
∴PN=|AP-AN|=|3t-8|=2$\sqrt{7}$,
∴t=$\frac{8±2\sqrt{7}}{3}$.
即:时间为$\frac{8±2\sqrt{7}}{3}$.时,△PCD是直角三角形.
点评 此题是四边形的综合题,主要考查矩形的判定,勾股定理,直角三角形的性质,解本题的关键是得出点P到线段CD中点的距离等于CD的一半.

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
14.已知x2+y2=2,x+y=1,则xy的值为( )
| A. | -$\frac{1}{2}$ | B. | -1$\frac{1}{2}$ | C. | -1 | D. | 3 |
6.(2x-1)2=(3x+2)2的解为( )
| A. | x=-3 | B. | x=-$\frac{1}{5}$ | C. | x=$\frac{3}{5}$或x=-3 | D. | x=-3或x=-$\frac{1}{5}$ |
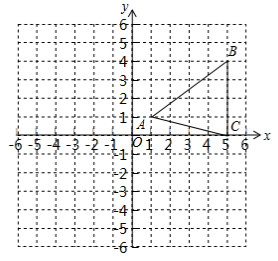 如图,在平面直角坐标系中,△ABC的顶点为A(1,1),B(5,4),C(5,0).
如图,在平面直角坐标系中,△ABC的顶点为A(1,1),B(5,4),C(5,0).