题目内容
5．若m＞0，且m-$\frac{1}{m}$=3，则m+$\frac{1}{m}$等于（ ）| A． | $\sqrt{10}$ | B． | $\sqrt{15}$ | C． | $\sqrt{13}$ | D． | $\sqrt{11}$ |
分析 根据完全平方公式即可求出答案．
解答 解：∵（m-$\frac{1}{m}$）2=9，
∴m2-2+$\frac{1}{{m}^{2}}$=9，
∴m2+$\frac{1}{{m}^{2}}$=11
∴m2+2+$\frac{1}{{m}^{2}}$=13
∴（m+$\frac{1}{m}$）2=13，
∵m＞0，
∴m+$\frac{1}{m}$=$\sqrt{13}$，
故选（C）
点评 本题考查完全平方公式，解题的关键是熟练运用完全平方公式，本题属于基础题型．
练习册系列答案
小学期末标准试卷系列答案
相关题目
13．下列计算，正确的是（ ）
| A． | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B． | |$\frac{1}{2}$-2|=-$\frac{3}{2}$ | C． | $\root{3}{8}$=2$\sqrt{2}$ | D． | （$\frac{1}{2}$）-1=2 |
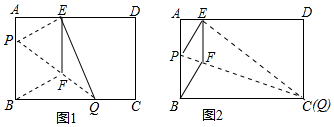
14．
为测量操场上旗杆的高度，小丽同学想到了物理学中平面镜成像的原理．她拿出随身携带的镜子和卷尺，先将镜子放在脚下的地面上，然后后退，直到她站直身子刚好能从镜子里看到旗杆的顶端E，标记好脚掌中心位置为B，测得脚掌中心位置B到镜面中心C的距离是50cm，镜面中心C距离旗杆底部D的距离为4m，如图所示．已知小丽同学的身高是1.54m，眼睛位置A距离小丽头顶的距离是4cm，则旗杆DE的高度等于（ ）
为测量操场上旗杆的高度，小丽同学想到了物理学中平面镜成像的原理．她拿出随身携带的镜子和卷尺，先将镜子放在脚下的地面上，然后后退，直到她站直身子刚好能从镜子里看到旗杆的顶端E，标记好脚掌中心位置为B，测得脚掌中心位置B到镜面中心C的距离是50cm，镜面中心C距离旗杆底部D的距离为4m，如图所示．已知小丽同学的身高是1.54m，眼睛位置A距离小丽头顶的距离是4cm，则旗杆DE的高度等于（ ）| A． | 10m | B． | 12m | C． | 12.4m | D． | 12.32m |
10．
如图，一条直线AB上有一点O，∠AOM=90°，∠COD=90°，∠COD在平角∠AOB内左右摆动（O点不动，OC与OA、OD与OB均不重合），在摆动时，除直角外，保持相等的角有（ ）
如图，一条直线AB上有一点O，∠AOM=90°，∠COD=90°，∠COD在平角∠AOB内左右摆动（O点不动，OC与OA、OD与OB均不重合），在摆动时，除直角外，保持相等的角有（ ）| A． | 一对 | B． | 两对 | C． | 三对 | D． | 四对 |
17．在平面直角坐标系中，点P（-1，2）向上平移3个单位长度后的坐标是（ ）
| A． | （2，2） | B． | （-4，2） | C． | （-1，5） | D． | （-1，-1） |
如图，∠AOD=90°，∠BOC=90°，图中互余的角有∠1和∠2；∠2和∠3．