题目内容
7.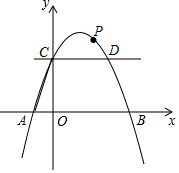 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,点A、B的坐标分别是(-1,0)、(5,0),与y轴交于点C,连接AC,过点C作CD∥x轴交抛物线于点D,点P是抛物线上一个动点,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,点A、B的坐标分别是(-1,0)、(5,0),与y轴交于点C,连接AC,过点C作CD∥x轴交抛物线于点D,点P是抛物线上一个动点,设点P的横坐标为m.(1)求抛物线的解析式;
(2)过点P作PQ∥AC交抛物线的对称轴于点Q,当PQ=AC时,求m的值;
(3)设以O、C、D、P为顶点的四边形的面积为S,当点P在y轴右侧的抛物线上时,求S与m之间的函数关系式;
(4)M是x轴上的一点,若以A、C、M、P为顶点的四边形是平行四边形时,求点M的坐标.
分析 (1)利用待定系数法即可解决问题;
(2)分P在对称轴左右两侧讨论即可;
(3)分点P在点D的上方或下方两种情形讨论即可解决问题.
(4)以A、C、M、P为顶点的四边形是平行四边形有四种情形,分别求解即可.
解答 解:(1)把A(-1,0),B(5,0)代入y=-$\frac{1}{2}$x2+bx+c可得
$\left\{\begin{array}{l}{-\frac{1}{2}-b+c=0}\\{-\frac{1}{2}×{5}^{2}+5b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=2}\\{c=\frac{5}{2}}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+2x+$\frac{5}{2}$.
(2)∵抛物线的解析式为y=-$\frac{1}{2}$x2+2x+$\frac{5}{2}$的对称轴x=2,
当点P在对称轴左侧时,如图1中,2-m=1,m=1.
当点P在对称轴右侧时,如图2中,m-2=1,m=3.
(3)过点P作PE⊥CD于点E.
当0<m<2时,如图3中,S=$\frac{1}{2}$×4×(-$\frac{1}{2}$m2+2m+$\frac{5}{2}$-$\frac{5}{2}$)+$\frac{1}{2}$×4×$\frac{5}{2}$=-m2+4m+5.
当m>4时,S=$\frac{1}{2}$×4×($\frac{5}{2}$+$\frac{1}{2}$m2-2m-$\frac{5}{2}$)+$\frac{1}{2}$m×$\frac{5}{2}$=m2-$\frac{11}{4}$m.
(4)①如图5中,当P1与D重合时,四边形ACDM1是平行四边形,易知AM1=CD=4,∴M1(3,0).
②如图6中,当四边形ACM2P2是平行四边形时,作P2H⊥x轴于H.
由△ACO≌△M2P2H,可得P2H=OC=$\frac{5}{2}$,M2H=OA=1,
当y=-$\frac{5}{2}$时,-$\frac{1}{2}$x2+2x+$\frac{5}{2}$=-$\frac{5}{2}$,解得x=2±$\sqrt{14}$,
∴OH=2+$\sqrt{14}$,M2(3+$\sqrt{14}$,0).
③如图7中,当AC是平行四边形DCM3A的对角线时,易知M3(-5,0).
④如图8中,当四边形ACM4P4是平行四边形时,同法可得M4(3-$\sqrt{14}$,0).
点M的坐标为(3,0)或(3+$\sqrt{14}$,0)或(-5,0)或(3-$\sqrt{14}$,0).
点评 本题考查二次函数综合题、平行四边形的判定和性质、四边形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | (2,2) | B. | (-4,2) | C. | (-1,5) | D. | (-1,-1) |
| A. |  | B. |  | C. |  | D. |  |
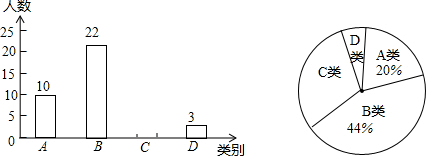
 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.| 分数段 (分数为x分) | 频数 | 百分比 |
| 60≤x<70 | 8 | 20% |
| 70≤x<80 | a | 30% |
| 80≤x<90 | 16 | b% |
| 90≤x<100 | 4 | 10% |
(1)表中的a=12,b=40;
(2)请补全频数分布直方图;
(3)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应的圆心角的度数是108°;
(4)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽取2名同学接受电视台记者采访,请用列表或画树状图的方法求正好抽到一名男同学和一名女同学的概率.
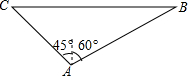 如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为(40+40$\sqrt{3}$)海里.
如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为(40+40$\sqrt{3}$)海里.
 已知:一小球在如图所示正方形区域滚动,正方形ABCD边长为3,E、F、G、H分别为各边上的点,且AE=BF=CG=DH=1,则小球停止后正好落在阴影区域的概率是$\frac{5}{9}$.
已知:一小球在如图所示正方形区域滚动,正方形ABCD边长为3,E、F、G、H分别为各边上的点,且AE=BF=CG=DH=1,则小球停止后正好落在阴影区域的概率是$\frac{5}{9}$.