��Ŀ����
17����ͼ������ABCD�У�AB��CD����ABC=90�㣬AB=6��BC=8��tanD=2����E������CD��һ���㣨�����C�غϣ�������BCE����BE���з��ۣ���C�Ķ�Ӧ���Ϊ��F����1����ͼ1������F��������ABCD����λ��MN��ʱ����CE�ij���
��2����ͼ2������E���߶�CD��ʱ����CE=x��$\frac{{{S_{��BFC}}}}{{{S_{��EFC}}}}$=y����y��x֮��ĺ�����ϵʽ����д��������
��3����ͼ3������AC���߶�BF������CA���ڵ�G������CBG�ǵ���������ʱ����CE�ij���
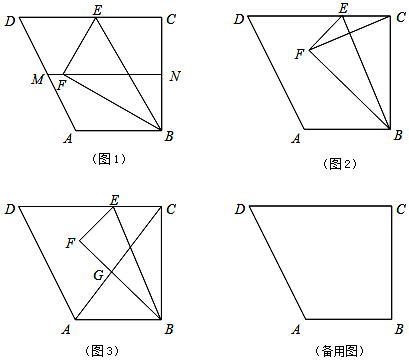
���� ��1����BE��MN�Ľ����Ϊ��O�������۵��������Լ�������λ�߶��������ж���EFO�ǵȱ������Σ����ɵó���FEB=60�㣬��CEB=60�㣬���ɵó���Rt��ECB�У�$EC=cot60��•BC=\frac{{\sqrt{3}}}{3}��8=\frac{{8\sqrt{3}}}{3}$��
��2����BE��CF�Ľ����Ϊ��P������BE��CF�Ĵ�ֱƽ���ߣ��ɵ�S��EFC=2S��EPC��S��BFC=2S��BPC�������õ�$\frac{{{S_{��BFC}}}}{{{S_{��EFC}}}}=\frac{{{S_{��BPC}}}}{{{S_{��EPC}}}}$�����ж���ECP�ס�CBP���ɵ�$\frac{{{S_{��BPC}}}}{{{S_{��EPC}}}}={��\frac{BC}{EC}��^2}={��{\frac{8}{x}}��^2}=\frac{64}{x^2}$�����ɵó�$y=\frac{{{S_{��BFC}}}}{{{S_{��EFC}}}}=\frac{64}{x^2}$��0��x��10����
��3������CBG�ǵ���������ʱ������������������ۣ���GB=GC����CB=CG����BC=BG���ֱ�����۵��������Լ�ֱ�������εı߽ǹ�ϵ�����CE�ij���
���  �⣺��1����BE��MN�Ľ����Ϊ��O��
�⣺��1����BE��MN�Ľ����Ϊ��O��
������ABCD�У�AB��CD����ABC=90�㣬
���C=90�㣬
�ɷ��۵á�CEB=��FEB����EFB=��C=90�㣬
��MN������ABCD����λ�ߣ�
��MN��AB��CD��
���CEB=��FOE��$\frac{EO}{OB}=\frac{CN}{BN}=1$��
���FEB=��FOE��
��FE=FO��
�ߡ�EFB=90�㣬EO=BO��
��FO=EO��
��FE=FO=EO��
���EFO�ǵȱ������Σ�
���FEB=60�㣬
���CEB=60�㣬
����Rt��ECB�У�$EC=cot60��•BC=\frac{{\sqrt{3}}}{3}��8=\frac{{8\sqrt{3}}}{3}$��
��2����BE��CF�Ľ����Ϊ��P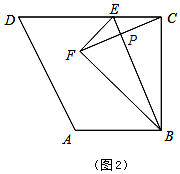 ��
��
�ɷ��۵ã�BE��CF�Ĵ�ֱƽ���ߣ�
����EPC=��BPC=90�㣬$FP=CP=\frac{1}{2}FC$��
��S��EFC=2S��EPC��S��BFC=2S��BPC��
��$\frac{{{S_{��BFC}}}}{{{S_{��EFC}}}}=\frac{{{S_{��BPC}}}}{{{S_{��EPC}}}}$��
�ߡ�ECP+��BCP=90�㣬��CBP+��BCP=90�㣬
���ECP=��CBP��
�֡ߡ�EPC=��BPC=90�㣬
���ECP�ס�CBP��
��$\frac{{{S_{��BPC}}}}{{{S_{��EPC}}}}={��\frac{BC}{EC}��^2}={��{\frac{8}{x}}��^2}=\frac{64}{x^2}$
��$y=\frac{{{S_{��BFC}}}}{{{S_{��EFC}}}}=\frac{64}{x^2}$��0��x��10����
��3������CBG�ǵ���������ʱ���������������
��GB=GC��
�ӳ�BF��CD�ڵ�H ��
��
��GB=GC��
���GBC=��GCB��
�ߡ�HCB=90�㣬
���CHB+��GBC=90�㣬
�ߡ�ABC=90�㣬
���CAB+��GCB=90�㣬
���CHB=��CAB��
��sin��CHB=sin��CAB=$\frac{4}{5}$��
�ߡ�ABC=90�㣬
���ACB+��CAB=90�㣬��ABG+��GBC=90�㣬
���CAB=��GBA��
��GA=GB��
��GA=GC��
��AB��CD��
��$\frac{CH}{AB}=\frac{CG}{AG}=1$��
��CH=AB=6��
��CE=x��
��EF=x��HE=6-x��
�ߡ�HFE=90�㣬
��$sin��CHB=\frac{EF}{HE}=\frac{x}{6-x}=\frac{4}{5}$��
���$x=\frac{8}{3}$����$CE=\frac{8}{3}$��
��CB=CG��
��CB=CG=8ʱ��AG=10-8=2��
��AB��CD��
��$\frac{CH}{AB}=\frac{CG}{AG}=4$��
��CH=4AB=24��
��CE=x��
��EF=x��HE=24-x��
�ߡ�HFE=��HCB=90�㣬
��$sin��CHB=\frac{EF}{HE}=\frac{BC}{BH}=\frac{x}{24-x}=\frac{1}{{\sqrt{10}}}$��
���$x=\frac{{8\sqrt{10}-8}}{3}$����$CE=\frac{{8\sqrt{10}-8}}{3}$��
��BC=BG��
��BC=BGʱ��F����G���غ� ��
��
�ɷ��ۿɵã�BE��ֱƽ���߶�GC��
�ߡ�CBE+��BCA=90��=��CAB+��BCA��
���CBE=��CAB��
�ߡ�ECB=��CBA=90�㣬
��$tan��CBE=tan��CAB=\frac{4}{3}$��
��$\frac{CE}{8}=\frac{4}{3}$��
���CE=$\frac{32}{3}$��
����������CE�ij�Ϊ$\frac{8}{3}$��$\frac{{8\sqrt{10}-8}}{3}$��$\frac{32}{3}$��
���� ���������ı����ۺ��⣬��Ҫ���������ε����ʣ��ȱ������ε��ж������ʣ����������ε��ж������ʣ��߶δ�ֱƽ���ߵ������Լ�ƽ���߷��߶γɱ����������ۺ�Ӧ�ã��������Ĺؼ��ǻ���ͼ�Σ������з������ۣ�����ʱע�⣺���������ε����֮�ȵ������Ʊȵ�ƽ����

 ��У����ϵ�д�
��У����ϵ�д�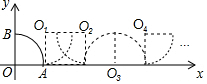 ��ͼ����A��2��0����B��0��2����������AOB��x���������������Ĺ������ڹ��������е�O�Ķ�Ӧ�����μ�Ϊ��O1����O2����O3������O10�������ǣ�������
��ͼ����A��2��0����B��0��2����������AOB��x���������������Ĺ������ڹ��������е�O�Ķ�Ӧ�����μ�Ϊ��O1����O2����O3������O10�������ǣ�������| A�� | ��16+4�У�0�� | B�� | ��14+4�У�2�� | C�� | ��14+3�У�2�� | D�� | ��12+3�У�0�� |
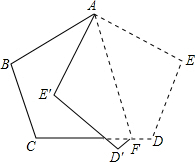 �������ֽƬABCDE����ͼ��ʽ�۵����ۺ�ΪAF����E��D�ֱ�����E�䣬D��㣮��֪��AFC=76�㣬���CFD����ڣ�������
�������ֽƬABCDE����ͼ��ʽ�۵����ۺ�ΪAF����E��D�ֱ�����E�䣬D��㣮��֪��AFC=76�㣬���CFD����ڣ�������| A�� | 15�� | B�� | 25�� | C�� | 28�� | D�� | 31�� |
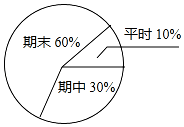 ����ı��������ͬѧһѧ����ѧ�ɼ��ļ�¼�����ݱ����ṩ����Ϣ�ش����������
����ı��������ͬѧһѧ����ѧ�ɼ��ļ�¼�����ݱ����ṩ����Ϣ�ش���������� | ������� | ƽʱ | ���п��� | ��ĩ���� | |||
| ��һ��Ԫ | �ڶ���Ԫ | ������Ԫ | ���ĵ�Ԫ | |||
| �ɼ� | 88 | 86 | 90 | 92 | 90 | 96 |
��2�����ͬѧ6�γɼ�����λ����90��
��3�����ͬѧƽʱ�ɼ���ƽ������89��
��4���������ͼ��Ȩ�ظ���մ�֣���Ӧ�õö��ٷ֣�������100�֣�д��������̣�
 ���Ķ����⡿����֪������a��0��b��0ʱ����$\sqrt{a}$-$\sqrt{b}$��2��0������a-2$\sqrt{ab}$+��0���Ӷ�a+b��2$\sqrt{ab}$����a=bʱȡ�Ⱥţ���
���Ķ����⡿����֪������a��0��b��0ʱ����$\sqrt{a}$-$\sqrt{b}$��2��0������a-2$\sqrt{ab}$+��0���Ӷ�a+b��2$\sqrt{ab}$����a=bʱȡ�Ⱥţ���