题目内容
17.若(a+b)2=12,(a-b)2=6,则ab的值是( )| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | 5 | D. | -5 |
分析 根据(a+b)2=12,(a-b)2=6,展开后然后两式作差即可求得ab的值,从而可以解答本题.
解答 解:∵(a+b)2=12,(a-b)2=6,
∴a2+2ab+b2=12,
a2-2ab+b2=6,
∴4ab=6,
得ab=$\frac{3}{2}$,
故选A.
点评 本题考查完全平方公式,解题的关键是明确完全平方公式,可以利用公式展开并作差求得所求式子的值.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
8.二次函数y=(x-3)2+2的顶点坐标是( )
| A. | (-3,-2) | B. | (3,2) | C. | (3,-2) | D. | (-3,1) |
5.已知y=(m-2)x|m|+2是y关于x的二次函数,那么m的值为( )
| A. | -2 | B. | 2 | C. | ±2 | D. | 0 |
12.某病毒的直径是0.000000068m,这个数据用科学计数法表示为( )
| A. | 6.8×10-7m | B. | 68×10-9m | C. | 0.68×10-7m | D. | 6.8×10-8m |
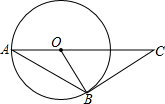 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=28°,则∠C的度数是34°.
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=28°,则∠C的度数是34°.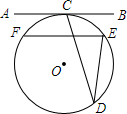 如图,直线AB与⊙O相切于点C,D是⊙O上的一点,∠CDE=22.5°,若EF∥AB,且EF=2,则⊙O的半径是$\sqrt{2}$.
如图,直线AB与⊙O相切于点C,D是⊙O上的一点,∠CDE=22.5°,若EF∥AB,且EF=2,则⊙O的半径是$\sqrt{2}$.