题目内容
9.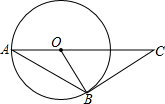 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=28°,则∠C的度数是34°.
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=28°,则∠C的度数是34°.
分析 首先利用等腰三角形的性质以及三角形外角的性质求得∠COB的度数,然后根据切线的性质可得△OBC是直角三角形,然后根据三角形的内角和定理求解即可.
解答 解:∵OA=OB,
∴∠A=∠ABO=28°,
∴∠COB=∠A+∠ABO=56°,
又∵BC是切线,
∴OB⊥BC,则∠OBC=90°,
∴∠C=90°-∠COB=90°-56°=34°.
故答案为34°.
点评 本题考查了切线的性质,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
17.若(a+b)2=12,(a-b)2=6,则ab的值是( )
| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | 5 | D. | -5 |
4.数据-3,-2,-2,-3,-1,-1,-2的众数和中位数分别是( )
| A. | -3;-3 | B. | -3;-2 | C. | -2;-3 | D. | -2;-2 |
11.下列说法正确的是( )
| A. | 近似数2.12万精确到十分位 | |
| B. | 经过两点有且只有一条直线 | |
| C. | 若ax=bx,则a=b | |
| D. | 若多项式5x|m|y2-(m-2)xy是四次二项式,则m=±2 |
 如图,图形2可以看作图形1先向下平移2格,再向左平移1格得到.
如图,图形2可以看作图形1先向下平移2格,再向左平移1格得到.


