题目内容
7.已知a、b都是有理数,且|a-1|+|b-2|=0,则a-b的值为-1.分析 根据非负数的性质列方程求出a、b的值,然后代入代数式进行计算即可得解.
解答 解:由题意得,a-1=0,b-2=0,
解得a=1,b=2,
所以,a-b=1-2=-1.
故答案为:-1.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
15.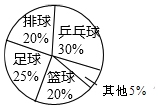 如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )
如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )
 如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )
如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )| A. | 该班喜欢乒乓球的学生最多 | |
| B. | 该班喜欢排球和篮球的学生一样多 | |
| C. | 该班喜欢足球的人数是喜欢排球人数的1.25倍 | |
| D. | 该班喜欢其他球类活动的人数为5人 |
19.某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送2450张照片,如果全班有x名同学,根据题意,列出方程为( )
| A. | x(x+1)=2450 | B. | x(x-1)=2450 | C. | $\frac{1}{2}$x(x+1)=2450 | D. | $\frac{1}{2}$x(x-1)=2450 |
17.下列各项中,结论正确的是( )
| A. | 若a>0,b<0,则$\frac{b}{a}$>0 | B. | 若a>b,则a-b>0 | ||
| C. | 若a<0,b<0,则ab<0 | D. | 若a>b,a<0,则$\frac{b}{a}$<0 |
 观察图形,利用图形面积关系用写出一个代数恒等式.
观察图形,利用图形面积关系用写出一个代数恒等式.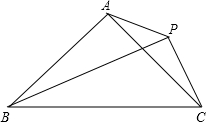 如图,等腰△ABC中,AB=AC,∠BAC=90°,P为△ABC外一点,PA=2$\sqrt{2}$,PB=7,PC=3.
如图,等腰△ABC中,AB=AC,∠BAC=90°,P为△ABC外一点,PA=2$\sqrt{2}$,PB=7,PC=3.